题目内容
 如图,平面直角坐标系中,直线AB与x轴、y轴分别交于A(3,0),B(0,
如图,平面直角坐标系中,直线AB与x轴、y轴分别交于A(3,0),B(0, )两点.
)两点.
(1)求直线AB的解析式;
(2)在第一象限内是否存在点P,使得以P、O、B为顶点的三角形与△OBA相似?若存在,请画出所有符合条件的点P,并求其中一个点P的坐标;若不存在,请说明理由.
解:(1)设函数解析式为y=kx+b,
根据题意 ,
,
解得 ,
,
∴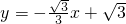 .
.
(2)过O作OP⊥AB垂足为P,得△OBA∽△PBO,
过B作BP″⊥y轴,使BP″=OA,连接OP″,得△OBA∽△BOP″,
过B作BP′⊥OP″,垂足为P′,得△OBA∽△P′OB,
由题可得OA=3,OB= ,AB=2
,AB=2 ,∠OAB=30°.
,∠OAB=30°.
①若△BOP∽△OBA,则∠BPO=∠BAO=30°,BP= OB=3,
OB=3,
∴P1(3, );
);
②若△BPO∽△OAB,则∠BOP=∠BAO=30°,OP= OB=1,
OB=1,
∴P2(1, );
);
③当∠OPB=90°时,
过点P作OP⊥BC(如图),此时△PBO∽△OAB,∠BOP=∠BAO=30°,过点P作PM⊥OA,
在Rt△PBO中,BP= OB=
OB= ,OP=
,OP= BP=
BP= ,
,
∵在Rt△PMO中,∠OPM=60°,
∴OM= OP=
OP= ,PM=
,PM= OM=
OM= ,
,
∴P3( ,
, );
);
④若△POB∽△OAB,则∠OBP=∠BAO=30°,∠P4OM=90°-(90°-30°)=30°,
∴P4M= OM=
OM= ,
,
∴P4( ,
, ).
).
当∠OPB=90°时,点P在x轴上,不符合要求.
故符合条件的点有四个:P1(3, ),P2(1,
),P2(1, ),P3(
),P3( ,
, ),P4(
),P4( ,
, ).
).
分析:(1)求出直线斜率k和截距b,直线解析式就可以写出了.
(2)△OBA中,已经有一直角,再找一锐角相等就可以了.
点评:待定系数法求一次函数解析式和直角三角形相似的判定方法是本题考查的两个知识点.
根据题意
 ,
,解得
 ,
,
∴
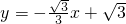 .
.(2)过O作OP⊥AB垂足为P,得△OBA∽△PBO,
过B作BP″⊥y轴,使BP″=OA,连接OP″,得△OBA∽△BOP″,
过B作BP′⊥OP″,垂足为P′,得△OBA∽△P′OB,
由题可得OA=3,OB=
 ,AB=2
,AB=2 ,∠OAB=30°.
,∠OAB=30°.
①若△BOP∽△OBA,则∠BPO=∠BAO=30°,BP=
 OB=3,
OB=3,∴P1(3,
 );
);②若△BPO∽△OAB,则∠BOP=∠BAO=30°,OP=
 OB=1,
OB=1,∴P2(1,
 );
);③当∠OPB=90°时,
过点P作OP⊥BC(如图),此时△PBO∽△OAB,∠BOP=∠BAO=30°,过点P作PM⊥OA,
在Rt△PBO中,BP=
 OB=
OB= ,OP=
,OP= BP=
BP= ,
,∵在Rt△PMO中,∠OPM=60°,

∴OM=
 OP=
OP= ,PM=
,PM= OM=
OM= ,
,∴P3(
 ,
, );
);④若△POB∽△OAB,则∠OBP=∠BAO=30°,∠P4OM=90°-(90°-30°)=30°,
∴P4M=
 OM=
OM= ,
,∴P4(
 ,
, ).
).当∠OPB=90°时,点P在x轴上,不符合要求.
故符合条件的点有四个:P1(3,
 ),P2(1,
),P2(1, ),P3(
),P3( ,
, ),P4(
),P4( ,
, ).
).分析:(1)求出直线斜率k和截距b,直线解析式就可以写出了.
(2)△OBA中,已经有一直角,再找一锐角相等就可以了.
点评:待定系数法求一次函数解析式和直角三角形相似的判定方法是本题考查的两个知识点.

练习册系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.