题目内容
 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
(1)求反比例函数的解析式及一次函数解析式;
(2)设一次函数y=kx+b的图象与x轴交于点C,连接OA,求△AOC的面积;
(3)结合图象,直接写出不等式kx+b>
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)把点A的坐标代入反比例函数解析式中,确定出反比例函数的解析式,再把点B的横坐标代入反比例函数解析式中得到点B的坐标,最后把点A和点B的坐标分别代入一次函数解析式中即可确定出一次函数解析式;
(2)利用一次函数解析式,令y=0,得到点C的坐标,求出OC的长,再利用点A纵坐标的绝对值即可求出三角形AOC的面积;
(3)结合图象,根据两函数的交点横坐标,将x轴分为4个范围,找出一次函数图象在反比例图象上方时x的范围即可.
(2)利用一次函数解析式,令y=0,得到点C的坐标,求出OC的长,再利用点A纵坐标的绝对值即可求出三角形AOC的面积;
(3)结合图象,根据两函数的交点横坐标,将x轴分为4个范围,找出一次函数图象在反比例图象上方时x的范围即可.
解答:解:(1)将A(-2,1)代入反比例解析式得:m=-2,
则反比例解析式为y=-
,
将B(1,n)代入反比例解析式得:n=-2,即(1,-2),
将A与B坐标代入y=kx+b得:
,
解得:
,
则一次函数解析式为y=-x-1;
(2)对于y=-x-1,令y=0求出x=-1,即OC=1,
则S△AOC=
×1×1=
;
(3)由图象得:-x-1>-
的解集为:x<-2或0<x<1.
则反比例解析式为y=-
| 2 |
| x |
将B(1,n)代入反比例解析式得:n=-2,即(1,-2),
将A与B坐标代入y=kx+b得:
|
解得:
|
则一次函数解析式为y=-x-1;
(2)对于y=-x-1,令y=0求出x=-1,即OC=1,
则S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图象得:-x-1>-
| 2 |
| x |
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2| 2 |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
 如图,在梯形ABCD中,AB∥DC,DE∥CB,若CD=4,△ADE周长为18,那么梯形ABCD的周长为( )
如图,在梯形ABCD中,AB∥DC,DE∥CB,若CD=4,△ADE周长为18,那么梯形ABCD的周长为( )| A、22 | B、26 | C、38 | D、30 |
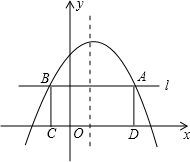 如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点(0,6),其对称轴为直线x=
如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点(0,6),其对称轴为直线x= 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=



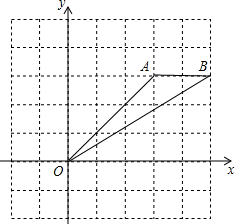 如图在平面直角坐标系中,已知点A(3,3),B(5,3).
如图在平面直角坐标系中,已知点A(3,3),B(5,3).