题目内容
如图1,抛物线y=ax2-3ax+b经过A(-1,0)、C(3,-2)两点,与y轴交于点D,与x轴交于另一点B.
(1)求此抛物线的解析式,并求出点B的坐标及抛物线的对称轴;
(2)点P为抛物线对称轴上一点,连接PA、PD,当△PAD的周长最小时,求点P的坐标;
(3)如图2,过点E(1,1)作EF⊥x轴于点F,将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与点A、E、F对),使点M、N在抛物线上,求点M、N的坐标.

解:(1)∵抛物线y=ax2-3ax+b经过A(-1,0)、C(3,-2)两点,
∴ ,
,
解得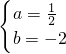 ,
,
∴抛物线解析式为y= x2-
x2- x-2,
x-2,
令y=0,则 x2-
x2- x-2=0,
x-2=0,
整理得,x2-3x-4=0,
解得x1=-1,x2=4,
∴点B的坐标为(4,0),
对称轴为直线x=- =-
=- =
= ,即x=
,即x= ;
;
(2)如图,连接BD,
∵A、B关于直线x= 对称,
对称,
∴BD与对称轴的交点即为△PAD的周长最小时的点P,
令x=0,则y=-2,
∴点D的坐标为(0,-2),
设直线BD的解析式为y=kx+m,将B(4,0),D(0,-2)代入得:
则 ,
,
解得 ,
,
所以,直线BD的解析式为y= x-2,
x-2,
当x= 时,y=
时,y= ×
× -2=-
-2=- ,
,
所以,点P的坐标为( ,-
,- );
);
(3)设对称中心坐标为(a,b),则点A(-1,0)的对称点M(2a+1,2b),
点E(1,1)的对称点N(2a-1,2b-1),
∵点M、N都在抛物线上,
∴ ,
,
①-②得,4a=4,
解得a=1,
把a=1代入①得, ×9-
×9- ×3-2=2b,
×3-2=2b,
解得b=-1,
∴方程组的解是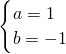 ,
,
∴点M(3,-2),N(1,-3).
分析:(1)把点A、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答,再令y=0,解关于x的一元二次方程求出点B的坐标,把二次函数对称轴公式进行计算即可得解;
(2)根据轴对称确定最短路线问题,连接BD,与对称轴的交点即为所求的点P,利用抛物线解析式求出点D的坐标,再利用待定系数法求一次函数解析式求出直线BD的解析式,然后解答即可;
(3)设对称中心的坐标为(a,b),根据中心对称的性质用a、b表示出点M、N的坐标,再根据点M、N在抛物线上,代入抛物线解析式得到关于a、b的方程组,求解得到a、b的值,从而得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式(包括二次函数解析式,一次函数解析式),抛物线与x轴的交点坐标的求解,求对称轴解析式,利用轴对称确定最短路线问题,(3)利用对称中心表示出点M、N的坐标是解题的关键,也是本题的难点.
∴
 ,
,解得
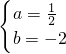 ,
,∴抛物线解析式为y=
 x2-
x2- x-2,
x-2,令y=0,则
 x2-
x2- x-2=0,
x-2=0,整理得,x2-3x-4=0,
解得x1=-1,x2=4,
∴点B的坐标为(4,0),
对称轴为直线x=-
 =-
=- =
= ,即x=
,即x= ;
;(2)如图,连接BD,
∵A、B关于直线x=
 对称,
对称,∴BD与对称轴的交点即为△PAD的周长最小时的点P,
令x=0,则y=-2,

∴点D的坐标为(0,-2),
设直线BD的解析式为y=kx+m,将B(4,0),D(0,-2)代入得:
则
 ,
,解得
 ,
,所以,直线BD的解析式为y=
 x-2,
x-2,当x=
 时,y=
时,y= ×
× -2=-
-2=- ,
,所以,点P的坐标为(
 ,-
,- );
);(3)设对称中心坐标为(a,b),则点A(-1,0)的对称点M(2a+1,2b),
点E(1,1)的对称点N(2a-1,2b-1),
∵点M、N都在抛物线上,
∴
 ,
,①-②得,4a=4,
解得a=1,
把a=1代入①得,
 ×9-
×9- ×3-2=2b,
×3-2=2b,解得b=-1,
∴方程组的解是
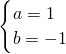 ,
,∴点M(3,-2),N(1,-3).
分析:(1)把点A、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答,再令y=0,解关于x的一元二次方程求出点B的坐标,把二次函数对称轴公式进行计算即可得解;
(2)根据轴对称确定最短路线问题,连接BD,与对称轴的交点即为所求的点P,利用抛物线解析式求出点D的坐标,再利用待定系数法求一次函数解析式求出直线BD的解析式,然后解答即可;
(3)设对称中心的坐标为(a,b),根据中心对称的性质用a、b表示出点M、N的坐标,再根据点M、N在抛物线上,代入抛物线解析式得到关于a、b的方程组,求解得到a、b的值,从而得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式(包括二次函数解析式,一次函数解析式),抛物线与x轴的交点坐标的求解,求对称轴解析式,利用轴对称确定最短路线问题,(3)利用对称中心表示出点M、N的坐标是解题的关键,也是本题的难点.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
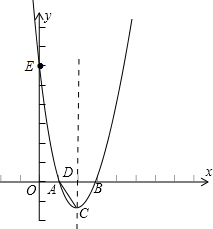 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
 如图,将抛物线
如图,将抛物线