题目内容
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
因为AB∥CD(已知),
所以∠AGF+______=180°(______ ),
因为GH平分∠AGF,MN平分∠CMG(______ ),
所以∠1=
∠AGF,∠2=
∠CMG(______),
得∠1+∠2=
(∠AGF+∠CMG)=______,
所以GH⊥MN(______).
根据已知条件和所得结论请总结出一个规律:______.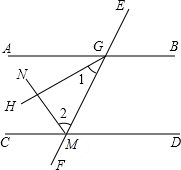
因为AB∥CD(已知),
所以∠AGF+______=180°(______ ),
因为GH平分∠AGF,MN平分∠CMG(______ ),
所以∠1=
| 1 |
| 2 |
| 1 |
| 2 |
得∠1+∠2=
| 1 |
| 2 |
所以GH⊥MN(______).
根据已知条件和所得结论请总结出一个规律:______.

∵AB∥CD(已知),
∴∠AGF+∠CHE=180°(两直线平行,同旁内角互补),
∵GH平分∠AGF,MN平分∠CMG(已知),
∴∠1=
∠AGF,∠2=
∠CMG(角平分线的定义),
得∠1+∠2=
(∠AGF+∠CMG)=90°,
∴GH⊥MN(垂直的定义).
根据已知条件和所得结论请总结出一个规律:两直线平行,同旁内角的角平分线互相垂直.
故答案为:∠CHE;两直线平行,同旁内角互补;已知;角平分线的定义;90°;垂直的定义;两直线平行,同旁内角的角平分线互相垂直.
∴∠AGF+∠CHE=180°(两直线平行,同旁内角互补),
∵GH平分∠AGF,MN平分∠CMG(已知),
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
得∠1+∠2=
| 1 |
| 2 |
∴GH⊥MN(垂直的定义).
根据已知条件和所得结论请总结出一个规律:两直线平行,同旁内角的角平分线互相垂直.
故答案为:∠CHE;两直线平行,同旁内角互补;已知;角平分线的定义;90°;垂直的定义;两直线平行,同旁内角的角平分线互相垂直.

练习册系列答案
相关题目
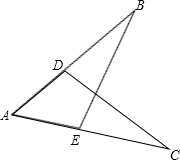 说理题:
说理题: 33、看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
33、看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?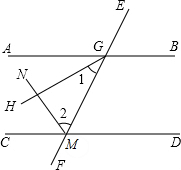 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.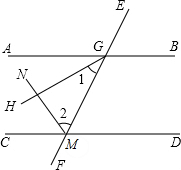 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由. ∠AGF,∠2=
∠AGF,∠2=