Question

【题目】如图，正方形面积为，延长至点，使得，以为边在正方形另一侧作菱形，其中，依次延长类似以上操作再作三个形状大小都相同的菱形，形成风车状图形，依次连结点则四边形的面积为___________．

Answer 1

【答案】

【解析】

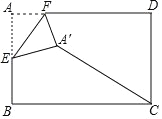
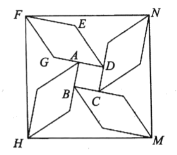
如图所示，延长CD交FN于点P，过N作NK⊥CD于点K，延长FE交CD于点Q，交NS于点R，首先利用正方形性质结合题意求出AD=CD=AG=DQ=1，然后进一步根据菱形性质得出DE=EF=DG=2，再后通过证明四边形NKQR是矩形得出QR=NK=，进一步可得，再延长NS交ML于点Z，利用全等三角形性质与判定证明四边形FHMN为正方形，最后进一步求解即可.

如图所示，延长CD交FN于点P，过N作NK⊥CD于点K，延长FE交CD于点Q，交NS于点R，

∵ABCD为正方形，

∴∠CDG=∠GDK=90°，

∵正方形ABCD面积为1，

∴AD=CD=AG=DQ=1，

∴DG=CT=2，

∵四边形DEFG为菱形，

∴DE=EF=DG=2，

同理可得：CT=TN=2，

∵∠EFG=45°，

∴∠EDG=∠SCT=∠NTK=45°，

∵FE∥DG，CT∥SN，DG⊥CT，

∴∠FQP=∠FRN=∠DQE=∠NKT=90°，

∴DQ=EQ=TK=NK=，FQ=FE+EQ=，

∵∠NKT=∠KQR=∠FRN=90°，

∴四边形NKQR是矩形，

∴QR=NK=，

∴FR=FQ+QR=，NR=KQ=DKDQ=，

∴，

再延长NS交ML于点Z，易证得：△NMZ△FNR(SAS)，

∴FN=MN，∠NFR=∠MNZ，

∵∠NFR+∠FNR=90°，

∴∠MNZ+∠FNR=90°，

即∠FNM=90°，

同理可得：∠NFH=∠FHM=90°，

∴四边形FHMN为正方形，

∴正方形FHMN的面积=，

故答案为：.