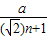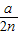题目内容
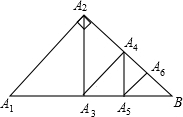 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,则线段A5A6的长为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,则线段A5A6的长为分析:根据等腰直角三角形的性质,运用勾股定理可知:A1A2=
A2A3,A2A3=
A3A4,从而能求出A5A6的值.
| 2 |
| 2 |
解答:解:∵△A1A2B是等腰直角三角形,A2A3⊥A1B,
∴△A1A2A3是等腰直角三角形,∴A1A2=
A2A3;
同理:△A2A3A4,△A3A4A5,△A4A5A6都是等腰直角三角形,
∴A2A3=
A3A4,A3A4=
A4A5,A4A5=
A5A6;
∵A1A2=4,∴A2A3=2
,A3A4=2,A4A5=
,A5A6=1.
故线段A5A6的长为1.
∴△A1A2A3是等腰直角三角形,∴A1A2=
| 2 |
同理:△A2A3A4,△A3A4A5,△A4A5A6都是等腰直角三角形,
∴A2A3=
| 2 |
| 2 |
| 2 |
∵A1A2=4,∴A2A3=2
| 2 |
| 2 |
故线段A5A6的长为1.
点评:灵活运用等腰直角三角形的性质,得到等腰直角三角形的斜边是直角边的
倍,从而准确得出结论.
| 2 |

练习册系列答案
相关题目
 如图,△A1A2B是等腰直角三角形,∠A1A2B=90°,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,…,An+1An+2⊥AnB,垂足为An+2(n为正整数),若A1A2=A2B=a,则线段An+1An+2的长为( )
如图,△A1A2B是等腰直角三角形,∠A1A2B=90°,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,…,An+1An+2⊥AnB,垂足为An+2(n为正整数),若A1A2=A2B=a,则线段An+1An+2的长为( )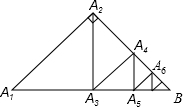 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,…以此类推,则线段A2nA2n+1(n为正整数)的长为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,…以此类推,则线段A2nA2n+1(n为正整数)的长为 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为 )n
)n