题目内容
 如图,线段AB、CD分别表示甲、乙两建筑物,从甲建筑物的顶部A处测得乙建筑物顶部C的仰角α=30°,底部D的俯角β=60°,如果要测量乙楼的高度CD,还需测得什么数据比较合理?请说明你的理由.
如图,线段AB、CD分别表示甲、乙两建筑物,从甲建筑物的顶部A处测得乙建筑物顶部C的仰角α=30°,底部D的俯角β=60°,如果要测量乙楼的高度CD,还需测得什么数据比较合理?请说明你的理由.
分析:需要测得BD的长比较合理.设BD=am,如图,过A作AE⊥CD于E,则分别可以得到AE=BD=am,CE=atanα,DE=atanβ,
所以得到CD=a(tanα+tanβ),由此即可求解.
所以得到CD=a(tanα+tanβ),由此即可求解.
解答: 解:测BD的长,
解:测BD的长,
设BD=am,
如图,过A作AE⊥CD于E,
∴AE=BD=am,
∵从甲建筑物的顶部A处测得乙建筑物顶部C的仰角α=30°,底部D的俯角β=60°,
则CE=atanα,DE=atanβ
∴CD=a(tanα+tanβ)=a(tan30°+tan45°)=(1+
)am.
∴需要测得BD的长比较合理.
 解:测BD的长,
解:测BD的长,设BD=am,
如图,过A作AE⊥CD于E,
∴AE=BD=am,
∵从甲建筑物的顶部A处测得乙建筑物顶部C的仰角α=30°,底部D的俯角β=60°,
则CE=atanα,DE=atanβ
∴CD=a(tanα+tanβ)=a(tan30°+tan45°)=(1+
| ||
| 3 |
∴需要测得BD的长比较合理.
点评:此题主要考查了解直角三角形的应用-仰角、俯角的问题,解题的关键正确理解仰角、俯角的定义,然后利用三角函数即可解决问题.

练习册系列答案
相关题目
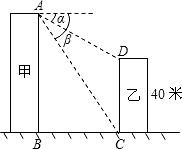 如图,线段AB,CD分别表示甲、乙两建筑物的高,AB⊥BC,CD⊥BC,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,已知乙建筑物高CD=40米.试求甲建筑物高AB.
如图,线段AB,CD分别表示甲、乙两建筑物的高,AB⊥BC,CD⊥BC,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,已知乙建筑物高CD=40米.试求甲建筑物高AB. 11、如图,线段AB=BC=CD=DE=1厘米,那么图中所有线段的长度之和等于
11、如图,线段AB=BC=CD=DE=1厘米,那么图中所有线段的长度之和等于
 6、如图,线段AB、CD互相平分于点O,过O作EF交AC于E,交BD于F,则这个图形是中心对称图形,对称中心是O.指出图形中的对应点
6、如图,线段AB、CD互相平分于点O,过O作EF交AC于E,交BD于F,则这个图形是中心对称图形,对称中心是O.指出图形中的对应点
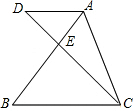 如图,线段AB、CD相交于E,AD∥BC,若AE:EB=1:2,S△ADE=1,则S△AEC等于
如图,线段AB、CD相交于E,AD∥BC,若AE:EB=1:2,S△ADE=1,则S△AEC等于 当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?
当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?