题目内容
一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，则k的取值范围是________．
k＜2且k≠1
分析：根据题意可得△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，再解方程与不等式即可．
解答：∵一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，
∴△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，
解得：k＜2，且k≠1，
故答案为：k＜2且k≠1．
点评：此题主要考查了一元二次方程根的情况与判别式，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
分析：根据题意可得△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，再解方程与不等式即可．
解答：∵一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，
∴△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，
解得：k＜2，且k≠1，
故答案为：k＜2且k≠1．
点评：此题主要考查了一元二次方程根的情况与判别式，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
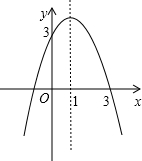已知二次函数y=-x2+bx+c的图象如图所示，解决下列问题：
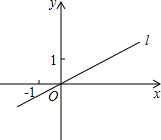如图，在平面直角坐标系中，直线l的解析式为y=