题目内容
 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为
- A.8 m
- B.4 m
- C.2 m
- D.6 m
B
分析:先根据30°角所对的直角边等于斜边的一半求出BC的长度,再根据三角形的中位线平行于第三边并且等于第三边的一半进行求解.
解答: 解:∵∠A=30°,AB=16m,
解:∵∠A=30°,AB=16m,
∴BC= AB=
AB= ×16=8m,
×16=8m,
∵BC、DE垂直于横梁AC,
∴BC∥DE,
∵点D是斜梁AB的中点,
∴DE= BC=
BC= ×8=4m.
×8=4m.
故选B.
点评:本题考查了30°角所对的直角边等于斜边的一半的性质以及三角形的中位线定理,熟记定理是解题的关键.
分析:先根据30°角所对的直角边等于斜边的一半求出BC的长度,再根据三角形的中位线平行于第三边并且等于第三边的一半进行求解.
解答:
 解:∵∠A=30°,AB=16m,
解:∵∠A=30°,AB=16m,∴BC=
 AB=
AB= ×16=8m,
×16=8m,∵BC、DE垂直于横梁AC,
∴BC∥DE,
∵点D是斜梁AB的中点,
∴DE=
 BC=
BC= ×8=4m.
×8=4m.故选B.
点评:本题考查了30°角所对的直角边等于斜边的一半的性质以及三角形的中位线定理,熟记定理是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为( )
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为( )| A、8m | B、4m | C、2m | D、6m |
 18、如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB=
18、如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB= 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=
如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=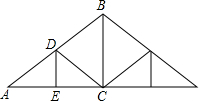 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为 如图是屋架设计图的一部分,∠ACB=90°,∠A=30°,若AB=8m,则BC=
如图是屋架设计图的一部分,∠ACB=90°,∠A=30°,若AB=8m,则BC=