题目内容
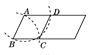
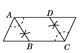
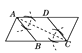
【题目】一位小朋友在粗糙不打滑的“![]() ”字形平面轨道上滚动一个半径为
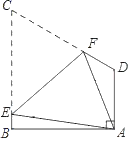
”字形平面轨道上滚动一个半径为![]() 的圆盘,如图所示,
的圆盘,如图所示,![]() 与
与![]() 是水平的,
是水平的,![]() 与水平面的夹角为
与水平面的夹角为![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
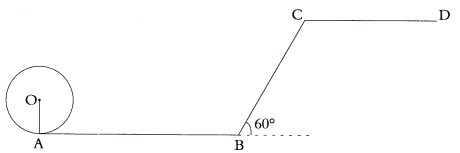
(1)小朋友将圆盘从点![]() 滚到与
滚到与![]() 相切的位置,此时圆盘的圆心
相切的位置,此时圆盘的圆心![]() 所经过的路线长为__________
所经过的路线长为__________![]() ;
;
(2)小朋友将圆盘从点![]() 滚动到点
滚动到点![]() ,其圆心所经过的路线长为__________
,其圆心所经过的路线长为__________![]() .
.
【答案】(60-![]() ) (140-
) (140-![]() +
+![]() )
)
【解析】
(1)作出圆心轨迹图,根据题意可知BE=BF,求出BE即可得到结果;
(2)圆心轨迹是AB+BC+CD-BE-BF+![]() ,计算即可.
,计算即可.

(1)当圆O与BC相切时,设圆O与BC的切点为E,圆O与AB的切点为F,则有BE=BF=![]() ,所以AE=60-
,所以AE=60-![]() ,
,
(2)在点C处旋转形成的圆弧所对的圆心角为60°,所以圆盘从点A滚动到点D其圆心所经过的路线=(60+40+40)-![]() ×2+
×2+![]() =140-
=140-![]() +
+![]() .
.

练习册系列答案
相关题目
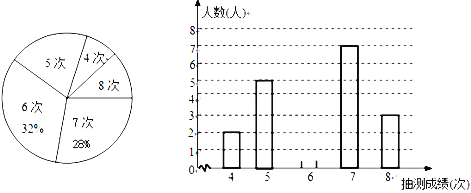
【题目】某地区九年级学生参加学业水平质量监测。随机抽取其中25名学生的成绩(满分为100分),统计如下:
90,74,88,65,98,75,81,42,85,70,55,80,95,88,72,88,60,56,76,66,78,72,82,63,100.
(1)90分及以上为![]() 级,75—89分为
级,75—89分为![]() 级,60—74分为
级,60—74分为![]() 级,60分以下为
级,60分以下为![]() 级。请把下面表格补充完整:
级。请把下面表格补充完整:
等级 |
|
|
|
|
人数 |
|
| 8 |
|
(2)根据(1)中完成的表格,可知这组数据的极差是____,中位数是____,众数是____.
(3)该地区某学校九年级共有1000名学生,如果60分及以上为及格,请估计该校九年级参加此次学业水平质量监测有多少人及格?
(4)若要知道抽测中每一个等级的人数占总人数的百分比,应选择_____统计图.