Question

【题目】如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．求证：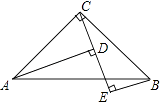

（1）△BEC≌△CDA；
（2）DE=AD﹣BE．

Answer 1

【答案】
（1）证明：∵∠ACD+∠BCE=90°，∠ACD+∠CAD=90°，

∴∠CAD=∠BCE，

在△CDA和△BEC中，

，

∴△CDA≌△BEC（AAS）

（2）证明：∵△CDA≌△BEC，

∴CD=BE，CE=AD，

∵DE=CE﹣CD，

∴DE=AD﹣BE

【解析】（1）易证∠CAD=∠BCE，即可证明△CDA≌△BEC，即可解题；（2）根据（1）中结论可得CD=BE，CE=AD，根据DE=CE﹣CD，即可解题．
【考点精析】通过灵活运用等腰直角三角形，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°即可以解答此题．