题目内容
 如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若△ABC的面积为7,DE=2,AB=4,则AC=
如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若△ABC的面积为7,DE=2,AB=4,则AC=3
3
.分析:首先根据角平分线上的点到角两边的距离相等可得DE=DF,再算出△ADB的面积,用△ABC的面积为-△ADB的面积可得到△ADC的面积,根据面积公式可计算出AC的长.
解答:解:∵AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F,
∴DE=DF,
∵DE=2,AB=4,
∴S△ADB=
•AB•DE=
×2×4=4,
∵△ABC的面积为7,
∴S△ADC=7-4=3,
∵
•DF•AC=3,
×2×AC=3,
AC=3,
故答案为:3.
∴DE=DF,
∵DE=2,AB=4,
∴S△ADB=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC的面积为7,
∴S△ADC=7-4=3,
∵
| 1 |
| 2 |
| 1 |
| 2 |
AC=3,
故答案为:3.
点评:此题主要考查了角平分线的性质,以及三角形的面积公式,关键是掌握角平分线上的点到角两边的距离相等得到DE=DF=2.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于
如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于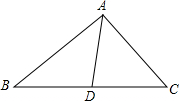 如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差.
如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差. 55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD.
55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD. 26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由.
26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由. 如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )
如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )