Question

【题目】如图，平面直角坐标系中，A（0，a）、B（b＋1，0），且a、b满足a2－12a＋＋36＝0，

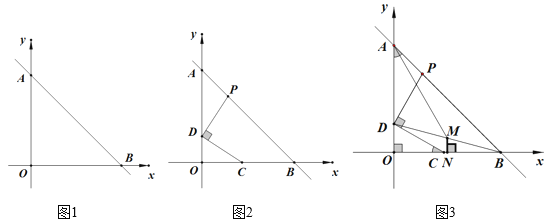
（1）求A、B两点的坐标；

（2）点C在线段BO上（C不与端点B、O重合），点D在线段AO上（D不与端点A、O重合），连CD，过D作CD的垂线交AB于P，若BC＝2DO，设C点横坐标为t，求P点横坐标（用含t的代数式表示）．

（3）在（2）的条件下，连BD， 点N是BO中点，NM⊥BO，交BD于点M，连AM，若BD＝PB，求AM的长．

Answer 1

【答案】（1）A(0，6)，B(6，0)；（2）点P的横坐标为；（3）AM=6；

【解析】

(1)由条件可得，求出a=6，b=5，则A、B两点的坐标可求；

（2）过点P作PE⊥0A于点E，证明，设PE=x，则，得出方程可求出x=，则P点的橫坐标可求出；

（3）求出直线AB的解析式，由（2）可知点P(，)，由PB=BD可求出，则.M(3，)，则AM的长可求出；

解：

（1）∵a2－12a＋＋36＝0，

∴，

∴a-6=0，b-5=0，

即a=6，b=5，

∴.A(0，6)，B(6，0)；

（2）过点P作PE⊥OA于点E，

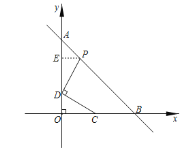
∵C点横坐标为t，BC=2DO，

∴DO=，

∵PD⊥DC，

∴∠PDC=90°，

∴∠PED=∠PDC=∠DOC=90°，

∴∠PDE=∠DCO，

∴，

∴，

设PE=x，则AE=x，DE=，

∴，

∴，

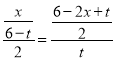∵t≠-6，

∴，

即点P的横坐标为；

（3）∵A(0，6)，B(6，0)，

∴设直线AB的解析式为y=kx+b，

∴，

解得，

∴直线AB的解析式为y=-x+6，

由（2）得点P(，)，

∵D（0，），B（6，0），

∴，，

∵PB=BD，

∴，

∴，

解得（负值舍去），

∵点N是BO中点，NM⊥BO，

∴M是BD的中点，

∴D(0，)，B(6，0)，

∴.M(3，)，

∴，

∴AM=6；