题目内容
当m________时,关于x的方程mx2+2(m+1)x+m-1=0有实数根.
≥-
分析:先要分类讨论:当m=0时,方程为一元一次方程,有一个实根;当m≠0时,原方程为一元二次方程,通过△≥0求m的范围;最后合并起来得到m的范围.
解答:当m=0时,原方程变为2x-1=0,此时原方程的实数根为x= ;
;
当m≠0时,原方程为一元二次方程,要使原方程有实根,只须△=4(m+1)2-4m(m-1)=12m+4≥0时,即m≥- .
.
所以当m≥- 时或当m=0时,原方程有实数根.
时或当m=0时,原方程有实数根.
故答案为≥- .
.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

分析:先要分类讨论:当m=0时,方程为一元一次方程,有一个实根;当m≠0时,原方程为一元二次方程,通过△≥0求m的范围;最后合并起来得到m的范围.
解答:当m=0时,原方程变为2x-1=0,此时原方程的实数根为x=
 ;
;当m≠0时,原方程为一元二次方程,要使原方程有实根,只须△=4(m+1)2-4m(m-1)=12m+4≥0时,即m≥-
 .
.所以当m≥-
 时或当m=0时,原方程有实数根.
时或当m=0时,原方程有实数根.故答案为≥-
 .
.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


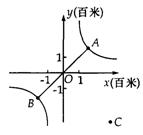
 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).