题目内容
9、如图，?ABCD中对角线AC、BD交点为O，AD=6，且△AOB周长比△BOC的周长多3，则?ABCD的周长为
30
．分析：首先根据平行四边形的性质得到AO=CO，AD=CB=6，AB=DC，再根据条件△AOB周长比△BOC的周长多3，得到AB=9，进而得到答案．
解答：解：∵四边形ABCD是平行四边形，
∴AO=CO，AD=CB=6，AB=DC
∵△AOB周长比△BOC的周长多3，
∴（AB+BO+AO）-（BO+BC+CO）=3，
即：AB-BC=3，
∴AB=6+3=9，
∴?ABCD的周长为：AB+BC+DC+AD=9+6+9+6=30．
故答案为：30．
∴AO=CO，AD=CB=6，AB=DC
∵△AOB周长比△BOC的周长多3，
∴（AB+BO+AO）-（BO+BC+CO）=3，
即：AB-BC=3，
∴AB=6+3=9，
∴?ABCD的周长为：AB+BC+DC+AD=9+6+9+6=30．
故答案为：30．
点评：此题主要考查了平行四边形的性质，解题的关键是根据条件△AOB周长比△BOC的周长多3得到AB的长．
练习册系列答案
相关题目
18、已知：如图梯形ABCD中，AD∥BC，AB=CD，AC与BD相交于点O．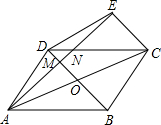
如图，?ABCD中，对角线AC，BD相交于点O，分别过D，C作DE∥OC，CE∥OD．
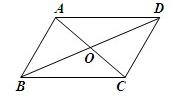9、如图，?ABCD中，O为AC、BD的中点，则图中全等的三角形共有（ ）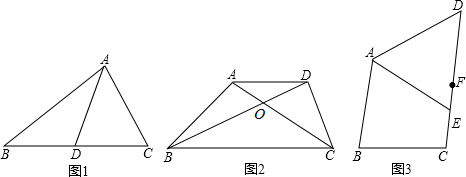
如图四边形ABCD中，CO=AO，BO=DO，AB与AD不相等，则图中有几对全等的三角形．（ ）