题目内容
 4、如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是
4、如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1
,点A关于x轴的对称点A′坐标是(-4,-1)
,点D坐标是(-4,3)
.分析:A到x轴的距离是点A的纵坐标的绝对值;
平面直角坐标系中任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),即关于横轴的对称点,横坐标不变,纵坐标变成相反数.这样就可以求出点A(-4,1)关于x轴对称的点的坐标是(-4,-1);
由于AD∥y轴,所以D点的横坐标与A点的横坐标相同,DC∥x轴,所以D点的纵坐标与C点的纵坐标相同.这样就可以求出点D坐标是(-4,3).
平面直角坐标系中任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),即关于横轴的对称点,横坐标不变,纵坐标变成相反数.这样就可以求出点A(-4,1)关于x轴对称的点的坐标是(-4,-1);
由于AD∥y轴,所以D点的横坐标与A点的横坐标相同,DC∥x轴,所以D点的纵坐标与C点的纵坐标相同.这样就可以求出点D坐标是(-4,3).
解答:解:∵A(-4,1),
∴点A到x轴的距离是1,
∴点A关于x轴的对称点A′坐标是(-4,-1),
∵B(0,1)、C(0,3),
∴CB=2,
∵四边形ABCD是矩形,
∴AD∥x轴,
∴D(-4,3)
故答案为:1,(-4,-1),(-4,3).
∴点A到x轴的距离是1,
∴点A关于x轴的对称点A′坐标是(-4,-1),
∵B(0,1)、C(0,3),
∴CB=2,
∵四边形ABCD是矩形,
∴AD∥x轴,
∴D(-4,3)
故答案为:1,(-4,-1),(-4,3).
点评:此题主要考查了平面直角坐标系关于坐标轴成轴对称的两点及平行于坐标轴的两点的坐标之间的关系,熟练掌握其规律是解题的关键.

练习册系列答案
相关题目
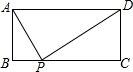 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
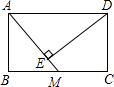 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.