Question

 已知△ABC中，∠C=90°，AC=BC=2，

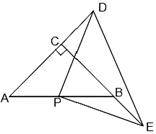
（1）如图1，如果点D，点E分别在边AC，BC上移动，在移动过程中保持CD=BE, 请判断△PDE的形状（无需说明理由）

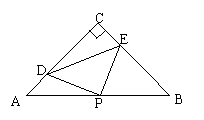
（2）如图2，如果点D,点E分别在AC，CB的延长线上移动，在移动过程中仍保持CD=BE，请问：（1）中的结论是否仍成立？若成立，请给予证明；若不成立，请说明理由。

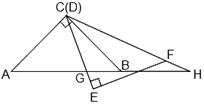
（3）如图3，将一块与△ABC全等的三角板如图放置（DE边与CB边重合），现将三角板绕点C顺时针旋转，当DF边与CA边重合时停止，不考虑起始和结束时情形，设DE，DF

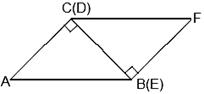
（或它们的延长线）分别交AB（或它的延长线）于G，H点（可参考图4），问BG长为多少时，△CGH是等腰三角形？（只需直接写出BG值）

图1                                         图2

	图3                                                 图4

Answer 1

（1）△PDE是等腰直角三角形------2分

  （2） 结论成立；连接CP，证△≌ △,得PD=PE---2分

        证∠=90，得△PDE是等腰直角三角形   -----2分

（3） 或                ----------2分