题目内容
 如图所示,S△ABC=1,若S△BDE=S△DEC=S△ACE,则S△ADE=
如图所示,S△ABC=1,若S△BDE=S△DEC=S△ACE,则S△ADE=
- A.

- B.

- C.

- D.

B
分析:由于S△BDE=S△DEC,利用两个三角形的高相等,那么底就相等,可得BD=DC,故可得出S△ABD= S△ABC=
S△ABC= ,由S△ABC=1,可知S△BDE=S△DEC=S△ACE=
,由S△ABC=1,可知S△BDE=S△DEC=S△ACE= ,由S△ADE=S△ABD-S△BDE即可得出结论.
,由S△ADE=S△ABD-S△BDE即可得出结论.
解答:∵S△BDE=S△DEC,
∴BD=DC,
∴S△ABD= S△ABC=
S△ABC= ,
,
∵S△ABC=1,S△BDE=S△DEC=S△ACE,
∴S△BDE=S△DEC=S△ACE= ,
,
∴S△ADE=S△ABD-S△BDE= -
- =
= .
.
故选B.
点评:本题考查了三角形是面积公式.注意同底等高的三角形面积相等,面积相等、同高的三角形底相等.
分析:由于S△BDE=S△DEC,利用两个三角形的高相等,那么底就相等,可得BD=DC,故可得出S△ABD=
 S△ABC=
S△ABC= ,由S△ABC=1,可知S△BDE=S△DEC=S△ACE=
,由S△ABC=1,可知S△BDE=S△DEC=S△ACE= ,由S△ADE=S△ABD-S△BDE即可得出结论.
,由S△ADE=S△ABD-S△BDE即可得出结论.解答:∵S△BDE=S△DEC,
∴BD=DC,
∴S△ABD=
 S△ABC=
S△ABC= ,
,∵S△ABC=1,S△BDE=S△DEC=S△ACE,
∴S△BDE=S△DEC=S△ACE=
 ,
,∴S△ADE=S△ABD-S△BDE=
 -
- =
= .
.故选B.
点评:本题考查了三角形是面积公式.注意同底等高的三角形面积相等,面积相等、同高的三角形底相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

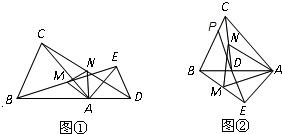 25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点. 24、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
24、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点. 9、如图所示,在△ABC中,AD,BE、CF交于点O,且AB=AC,AF=AE,BD=CD,则图中全等的三角形共有( )
9、如图所示,在△ABC中,AD,BE、CF交于点O,且AB=AC,AF=AE,BD=CD,则图中全等的三角形共有( ) 如图所示,在△ABC中,AB=AC,D是AB上任意一点,且BD=CE,连接DE交BC于F.
如图所示,在△ABC中,AB=AC,D是AB上任意一点,且BD=CE,连接DE交BC于F.