Question

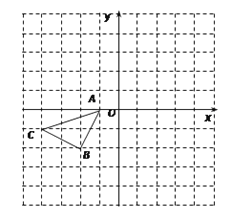
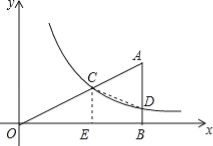
【题目】如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO=90°，∠AOB=30°，OB=2，反比例函数y=（x＞0）的图象经过OA的中点C，交AB于点D．

（1）求反比例函数的关系式；

（2）连接CD，求四边形CDBO的面积．

Answer 1

【答案】（1）y=；（2）

【解析】

试题分析：（1）解直角三角形求得AB，作CE⊥OB于E，根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标，然后根据待定系数法即可求得反比例函数的解析式；（2）求得D的坐标，进而求得AD的长，得出△ACD的面积，然后根据S四边形CDBO=S△AOB﹣S△ACD即可求得．

试题解析：（1）∵∠ABO=90°，∠AOB=30°，OB=2， ∴AB=OB=2， 作CE⊥OB于E，

∵∠ABO=90°， ∴CE∥AB， ∴OC=AC， ∴OE=BE=OB=，CE=AB=1， ∴C（，1），

∵反比例函数y=（x＞0）的图象经过OA的中点C， ∴1=， ∴k=，

∴反比例函数的关系式为y=；

（2）∵OB=2， ∴D的横坐标为2， 代入y=得，y=， ∴D（2，）， ∴BD=，

∵AB=2， ∴AD=， ∴S△ACD=ADBE=××=，

∴S四边形CDBO=S△AOB﹣S△ACD=OBAB﹣=×2×2﹣=．