题目内容
 如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y=
如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y= (x>0)的图象上,斜边OA1,A1A2都在x轴上,则点A2的坐标是________.
(x>0)的图象上,斜边OA1,A1A2都在x轴上,则点A2的坐标是________.
( ,0)
,0)
分析:作P1B⊥y轴,P1A⊥x轴,根据等腰直角三角形的性质解答即可.
解答: 解:作P1B⊥y轴,P1A⊥x轴,
解:作P1B⊥y轴,P1A⊥x轴,
∵△P1OA1,△P2A1A2是等腰直角三角形,
∴AP1=BP1,A1D=DA2=DP2,
则OA•OB=4,
∴OA=OB=AA1=2,OA1=4,
设A1D=x,则有(4+x)x=4,
解得x=-2+2 ,或x=-2-2
,或x=-2-2 (舍去),
(舍去),
则OA2=4+2x=4-4+4 =4
=4 ,A2坐标为(4
,A2坐标为(4 ,0).
,0).
点评:本题考查一定经过某点的函数应适合这个点的横纵坐标.
 ,0)
,0)分析:作P1B⊥y轴,P1A⊥x轴,根据等腰直角三角形的性质解答即可.
解答:
 解:作P1B⊥y轴,P1A⊥x轴,
解:作P1B⊥y轴,P1A⊥x轴,∵△P1OA1,△P2A1A2是等腰直角三角形,
∴AP1=BP1,A1D=DA2=DP2,
则OA•OB=4,
∴OA=OB=AA1=2,OA1=4,
设A1D=x,则有(4+x)x=4,
解得x=-2+2
 ,或x=-2-2
,或x=-2-2 (舍去),
(舍去),则OA2=4+2x=4-4+4
 =4
=4 ,A2坐标为(4
,A2坐标为(4 ,0).
,0).点评:本题考查一定经过某点的函数应适合这个点的横纵坐标.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
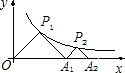 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=| 4 |
| x |
A、(2
| ||
B、(2
| ||
C、(4
| ||
D、(2
|
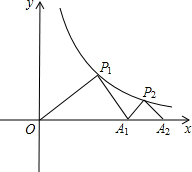 如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y=
如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y= 如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=
如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y= 如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数
如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数