Question

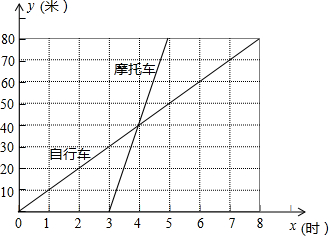
如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象（分别为正比例函数和一次函数）.两地间的距离是80千米.请你根据图象回答或解决下面的问题：

（1）谁出发的较早？早多长时间？谁到达乙地较早？早到多长时间？

（2）两人在途中行驶的速度分别是多少？

（3）请你分别求出表示自行车和摩托车行驶过程的函数解析式（不要求写出自变量的取值范围）；

（4）指出在什么时间段内两车均行驶在途中（不包括端点）；在这一时间段内，请你分别按下列条件列出关于时间x的方程或不等式（不要化简，也不要求解）：①自行车行驶在摩托车前面；②自行车与摩托车相遇；③自行车行驶在摩托车后面.

 

Answer 1

【答案】

（1）自行车出发早3个小时，摩托车到达乙地早3个小时 

（2）10千米/时，40千米/时

（3）自行车：y=10x，摩托车：y=40x－120

（4）在3＜x＜5时间段内两车均都行驶在途中，自行车在摩托车前面：10x＞40x－120，相遇：10x=40x－120，自行车在摩托车后：10x＜40x－120

【解析】

试题分析：（1）（2）可根据图象的信息得出结果．

（3）可先设出两条函数式的通式，然后根据待定系数法求解．

（4）要注意x的不同取值范围代表的不同含义，分情况进行讨论．

（1）由图可以看出，自行车出发较早，早3个小时，摩托车到达乙地较早，早3个小时．

（2）对自行车而言，行驶的距离是80千米，耗时8个小时．

所以其速度是：80÷8=10（千米/小时）；

对摩托车而言，行驶的距离是80千米，耗时2个小时．

所以其速度是：80÷2=40（千米/小时）．

（3）设表示自行车行驶过程的函数解析式为y=kx．

x=8时，y=80

因此k=10

∴表示自行车行驶过程的函数式是y=10x．

设表示摩托车行驶过程的函数解析式是y=ax+b

由题意可知：，解得

∴表示摩托车行驶过程的函数解析式为y=40x-120．

（4）再3＜x＜5时间段内两次均行驶在途中．

自行车在摩托车前：10x＞40x-120

两车相遇：10x=40x-120．

自行车在摩托车的后面：10x＜40x-120．

考点：本题考查的是一次函数的应用

点评：本题是利用一次函数的有关知识解答实际应用题，借助函数图象表达题目中的信息，读懂图象是关键．