题目内容
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC= , 若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M= . 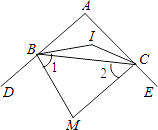
【答案】140°;40°
【解析】解:∵∠A=100°, ∵∠ABC+∠ACB=180°﹣100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC= ![]() ∠ABC,∠ICB=
∠ABC,∠ICB= ![]() ∠ACB,
∠ACB,
∴∠IBC+∠ICB= ![]() ∠ABC+
∠ABC+ ![]() ∠ACB=
∠ACB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×80°=40°,
×80°=40°,
∴∠I=180°﹣(∠IBC+∠ICB)=180°﹣40°=140°;
∵∠ABC+∠ACB=80°,
∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣80°=280°,
∵BM、CM分别平分∠ABC,∠ACB的外角平分线,
∴∠1= ![]() ∠DBC,∠2=
∠DBC,∠2= ![]() ECB,
ECB,
∴∠1+∠2= ![]() ×280°=140°,
×280°=140°,
∴∠M=180°﹣∠1﹣∠2=40°.
故答案为:140°;40°.
首先根据三角形内角和求出∠ABC+∠ACB的度数,再根据角平分线的性质得到∠IBC= ![]() ∠ABC,∠ICB=
∠ABC,∠ICB= ![]() ∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
根据∠ABC+∠ACB的度数,算出∠DBC+∠ECB的度数,然后再利用角平分线的性质得到∠1= ![]() ∠DBC,∠2=
∠DBC,∠2= ![]() ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.
ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目