Question

已知二次函数的图象经过点（0、3），且顶点坐标为（-1、4）
（1）求这个函数解析式
（2）在直角坐标系，画出它的图象
（3）根据图象说明：当x为何值时，函数值y为0？当x为何值时，函数y随x的增大而增大？当x时为何值时，函数y随x的增大而减少？

Answer 1

解：（1）设此二次函数的解析式为y=a（x+1）²+4．
∵其图象经过点（0，3），
∴a（0+1）²+4=3，
∴a=-1，
∴y=-（x+1）²+4=-x²-2x+1．

（2）根据题意得：


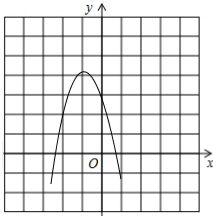
（3）由图可知，当y=0时，有-x²-2x+1=0，
解得，x₁=-1-，x₂=-1．
-1-＜x＜-1时，y＞0，
当x＜-1-或 x＞-1 时，y＜0．
分析：（1）已知二次函数的顶点坐标为（-1，4），设抛物线的顶点式为y=a（x+1）²+4，将点（0，3）代入求a即可．
（2）根据（1）所求出的解析式即可画出图象；
（3）根据（1）得出的二次函数关系式，解出当y=0时x的值，再根据顶点坐标画出图象，由图象直接得出答案即可．
点评：本题考查了用顶点式求抛物线解析式的一般方法，必须熟练掌握抛物线解析式的几种形式及抛物线与x轴的交点坐标等性质，要充分利用数形结合思想解答．