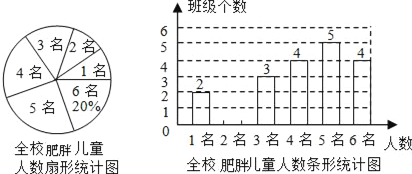
题目内容
【题目】已知正六边形的边心距为
，求正六边形的中心角、边长、周长和面积．
【答案】六边形的中心角为60°，边长为2，周长为12，面积为6
.
【解析】
试题首先根据题意作出图形，然后可得△OBC是等边三角形，然后由三角函数的性质，求得OB的长，继而求得正六边形的中心角、边长、周长和面积．
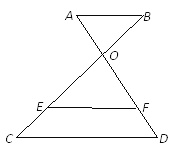
试题解析：如图，连接OB、OC，过点O作OH⊥BC于点H，
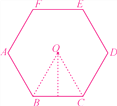
∵六边形ABCDEF是正六边形，∴∠BOC＝
×360°＝60°.
∵OB＝OC，∴△OBC是等边三角形．
∴∠OBC＝60°，BC＝OB＝OC.
∵OH＝
,sin∠OBC＝
，
∴OB＝BC＝2.
∴正六边形的周长为2×6＝12.
∴S正六边形ABCDEF＝6S△OBC＝6×
×2× 
＝6 .
∴正六边形的中心角为60°，边长为2，周长为12，面积为6.
练习册系列答案
相关题目
