题目内容
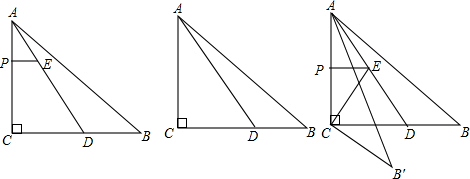
 如图,E是BC边上一点,AB⊥CB于点B,CD⊥CB于点C,AB=CB,∠A=∠CBD,AE与BD相交于点O,下列结论:①AE=BD;②AE⊥BD;③EB=CD;④△ABO的面积等于四边形CDOE的面积,其中正确的结论有________(填序号).
如图,E是BC边上一点,AB⊥CB于点B,CD⊥CB于点C,AB=CB,∠A=∠CBD,AE与BD相交于点O,下列结论:①AE=BD;②AE⊥BD;③EB=CD;④△ABO的面积等于四边形CDOE的面积,其中正确的结论有________(填序号).
①②③④
分析:根据ASA证△ABE≌△BCD,推出①②正确;根据三角形内角和定理求出∠CBD+∠AEB=90°,求出∠BOE=90°,即可判断③;根据全等三角形性质求出△ABE、△BCD面积相等,都减去△BOE的面积,即可判断④.
解答:∵AB⊥CB,CD⊥CB,
∴∠ABE=∠BCD=90°,
在△ABE和△BCD中
 ,
,
∴△ABE≌△BCD,
∴AE=BD,EB=CD∴①正确;③正确;
∵∠ABE=90°,
∴∠A+∠AEB=90°,
∵∠A=∠CBD,
∴∠AEB+∠cbd=90°,
∴∠BOE=180°-90°=90°,
∴AE⊥BD,∴②正确;
∵△ABE≌△BCD,
∴△ABE的面积等于△BCD的面积,
∵△BOE的面积等于△BOE的面积,
∴△ABO的面积等于四边形CDOE的面积,∴④正确;
故答案为:①②③④.
点评:本题考查了全等三角形的性质和判定,三角形的面积的应用,关键是求出△ABE和△BCD全等,主要培养学生运用定理进行推理的能力.
分析:根据ASA证△ABE≌△BCD,推出①②正确;根据三角形内角和定理求出∠CBD+∠AEB=90°,求出∠BOE=90°,即可判断③;根据全等三角形性质求出△ABE、△BCD面积相等,都减去△BOE的面积,即可判断④.
解答:∵AB⊥CB,CD⊥CB,
∴∠ABE=∠BCD=90°,
在△ABE和△BCD中
 ,
,∴△ABE≌△BCD,
∴AE=BD,EB=CD∴①正确;③正确;
∵∠ABE=90°,
∴∠A+∠AEB=90°,
∵∠A=∠CBD,
∴∠AEB+∠cbd=90°,
∴∠BOE=180°-90°=90°,
∴AE⊥BD,∴②正确;
∵△ABE≌△BCD,
∴△ABE的面积等于△BCD的面积,
∵△BOE的面积等于△BOE的面积,
∴△ABO的面积等于四边形CDOE的面积,∴④正确;
故答案为:①②③④.
点评:本题考查了全等三角形的性质和判定,三角形的面积的应用,关键是求出△ABE和△BCD全等,主要培养学生运用定理进行推理的能力.

练习册系列答案
相关题目
 重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
重合),EF∥BD交AC于点F,EG∥AC交BD于点G. (2013•怀柔区一模)如图,在△ABC中,AD是BC边上的中线,分别过点C、B作射线AD的垂线段,垂足分别为E、F.求证:BF=CE.
(2013•怀柔区一模)如图,在△ABC中,AD是BC边上的中线,分别过点C、B作射线AD的垂线段,垂足分别为E、F.求证:BF=CE. (2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )
(2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( ) 如图,BD是等边△ABC一边上的高,延长BC至E,使CE=CD,
如图,BD是等边△ABC一边上的高,延长BC至E,使CE=CD,