̀âÄ¿ÄÚÈƯ
¡¾̀âÄ¿¡¿ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬¹ưµă![]() ¡¢
¡¢![]() ·Ö±đ×÷
·Ö±đ×÷![]() ÖáµÄ´¹Ïߣ¬´¹×ă·Ö±đΪ
ÖáµÄ´¹Ïߣ¬´¹×ă·Ö±đΪ![]() ¡¢
¡¢![]() £®
£®
(1)ÇóÖ±Ïß![]() ºÍÖ±Ïß
ºÍÖ±Ïß![]() µÄ½âÎöʽ£»
µÄ½âÎöʽ£»
(2)µă![]() ΪֱÏß
ΪֱÏß![]() ÉϵÄ̉»¸ö¶¯µă£¬¹ư
ÉϵÄ̉»¸ö¶¯µă£¬¹ư![]() ×÷
×÷![]() ÖáµÄ´¹Ïß½»Ö±Ïß
ÖáµÄ´¹Ïß½»Ö±Ïß![]() ÓÚµă
ÓÚµă![]() £¬ÊÇ·ñ´æÔÚƠâÑùµÄµă
£¬ÊÇ·ñ´æÔÚƠâÑùµÄµă![]() £¬Ê¹µẲÔ
£¬Ê¹µẲÔ![]() ¡¢
¡¢![]() ¡¢
¡¢![]() ¡¢
¡¢![]() Ϊ¶¥µăµÄËıßĐÎΪƽĐĐËıßĐΣ¿Èô´æÔÚ£¬Çó´Ëʱµă
Ϊ¶¥µăµÄËıßĐÎΪƽĐĐËıßĐΣ¿Èô´æÔÚ£¬Çó´Ëʱµă![]() µÄºá×ø±ê£»Èô²»´æÔÚ£¬Çë˵Ă÷ÀíÓÉ£»
µÄºá×ø±ê£»Èô²»´æÔÚ£¬Çë˵Ă÷ÀíÓÉ£»
(3)Èô![]() ÑØ
ÑØ![]() ·½Ị̈ƽ̉Æ(µă
·½Ị̈ƽ̉Æ(µă![]() ÔÚÏ߶Î
ÔÚÏ߶Î![]() ÉÏ£¬Ç̉²»Óëµă
ÉÏ£¬Ç̉²»Óëµă![]() ÖغÏ)£¬ÔÚƽ̉ƵĹư³̀ÖĐ£¬Éèƽ̉ƾàÀëΪ
ÖغÏ)£¬ÔÚƽ̉ƵĹư³̀ÖĐ£¬Éèƽ̉ƾàÀëΪ![]() £¬
£¬![]() Óë
Óë![]() Öص₫²¿·ÖµÄĂæ»ư¼ÇΪ
Öص₫²¿·ÖµÄĂæ»ư¼ÇΪ![]() £¬ÊÔÇó
£¬ÊÔÇó![]() Óë
Óë![]() µÄº¯Êư¹Øϵʽ£®
µÄº¯Êư¹Øϵʽ£®
¡¾´đ°¸¡¿£¨1£©y=-x+4£¬y=![]() x£»£¨2£©m=
x£»£¨2£©m=![]() »̣
»̣![]() £»£¨3£©S=
£»£¨3£©S=![]() .
.
¡¾½âÎö¡¿
£¨1£©ÀíÓÉ´ư¶¨ÏµÊư·¨¼´¿É½â¾öÎỀ⣻
£¨2£©Èçͼ1ÖĐ£¬ÉèM£¨m£¬![]() £©£¬ỘN£¨m£¬-m+4£©£®µ±AC=MNʱ£¬A¡¢C¡¢M¡¢NΪ¶¥µăµÄËıßĐÎΪƽĐĐËıßĐΣ¬¿ÉµĂ|-m+4-
£©£¬ỘN£¨m£¬-m+4£©£®µ±AC=MNʱ£¬A¡¢C¡¢M¡¢NΪ¶¥µăµÄËıßĐÎΪƽĐĐËıßĐΣ¬¿ÉµĂ|-m+4-![]() |=3£¬½â·½³̀¼´¿É£»
|=3£¬½â·½³̀¼´¿É£»
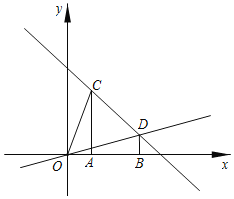
£¨3£©Èçͼ2ÖĐ£¬Éèƽ̉ÆÖеÄÈư½ÇĐÎΪ¡÷A¡äO¡äC¡ä£¬µăC¡äÔÚÏ߶ÎCDÉÏ£®ÉèO¡äC¡äÓëxÖá½»ÓÚµăE£¬ÓëÖ±ÏßOD½»ÓÚµăP£»ÉèA¡äC¡äÓëxÖá½»ÓÚµăF£¬ÓëÖ±ÏßOD½»ÓÚµăQ£®¸ù¾ƯS=S¡÷OFQ-S¡÷OEP=![]() OFFQ-
OFFQ-![]() OEPG¼ÆËă¼´¿É.
OEPG¼ÆËă¼´¿É.
½â£º£¨1£©ÉèÖ±ÏßCDµÄ½âÎöʽΪy=kx+b£¬ỘÓĐ![]() £¬½âµĂ
£¬½âµĂ![]() £¬
£¬
¡àÖ±ÏßCDµÄ½âÎöʽΪy=-x+4£®
ÉèÖ±ÏßODµÄ½âÎöʽΪy=mx£¬ỘÓĐ3m=1£¬m=![]() £¬
£¬
¡àÖ±ÏßODµÄ½âÎöʽΪy=![]() x.
x.
£¨2£©´æÔÚ£®
ÀíÓÉ£ºÈçͼ1ÖĐ£¬ÉèM£¨m£¬![]() £©£¬ỘN£¨m£¬-m+4£©£®
£©£¬ỘN£¨m£¬-m+4£©£®
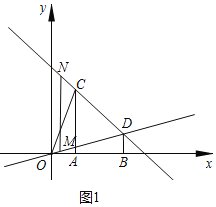
µ±AC=MNʱ£¬A¡¢C¡¢M¡¢NΪ¶¥µăµÄËıßĐÎΪƽĐĐËıßĐΣ¬
¡à|-m+4-![]() |=3£¬
|=3£¬
½âµĂm=![]() »̣
»̣![]() .
.
£¨3£©Èçͼ2ÖĐ£¬Éèƽ̉ÆÖеÄÈư½ÇĐÎΪ¡÷A¡äO¡äC¡ä£¬µăC¡äÔÚÏ߶ÎCDÉÏ£®
ÉèO¡äC¡äÓëxÖá½»ÓÚµăE£¬ÓëÖ±ÏßOD½»ÓÚµăP£»
ÉèA¡äC¡äÓëxÖá½»ÓÚµăF£¬ÓëÖ±ÏßOD½»ÓÚµăQ£®
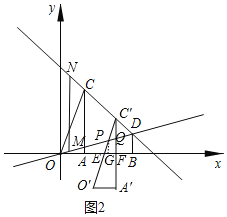
̣̉Ϊƽ̉ƾàÀëΪ![]() t£¬Ëù̉Ôˮƽ·½Ị̈µÄƽ̉ƾàÀëΪt£¨0¡Üt£¼2£©£¬
t£¬Ëù̉Ôˮƽ·½Ị̈µÄƽ̉ƾàÀëΪt£¨0¡Üt£¼2£©£¬
ỘͼÖĐAF=t£¬F£¨1+t£¬0£©£¬Q£¨1+t£¬![]() £©£¬C¡ä£¨1+t£¬3-t£©£®
£©£¬C¡ä£¨1+t£¬3-t£©£®
ÉèÖ±ÏßO¡äC¡äµÄ½âÎöʽΪy=3x+b£¬
½«C¡ä£¨1+t£¬3-t£©´úÈëµĂ£ºb=-4t£¬
¡àÖ±ÏßO¡äC¡äµÄ½âÎöʽΪy=3x-4t£®
¡àE£¨![]() £¬0£©£®
£¬0£©£®
ÁªÁ¢y=3x-4tÓëy=![]() £¬½âµĂx=
£¬½âµĂx=![]() £®
£®
¡àS=S¡÷OFQ-S¡÷OEP=![]() OFFQ-
OFFQ-![]() OEPG
OEPG
=![]() £¨1+t£©£¨
£¨1+t£©£¨![]() £©-
£©-![]()
=![]() .
.

 ¿ÎʱѵÁ·½ËƠÈËĂñ³ö°æÉçϵÁĐ´đ°¸
¿ÎʱѵÁ·½ËƠÈËĂñ³ö°æÉçϵÁĐ´đ°¸ »Æ¸Ô¾µäȤζ¿Î̀ĂϵÁĐ´đ°¸
»Æ¸Ô¾µäȤζ¿Î̀ĂϵÁĐ´đ°¸ Æô¶«Đ¡̀â×÷̉µ±¾ÏµÁĐ´đ°¸
Æô¶«Đ¡̀â×÷̉µ±¾ÏµÁĐ´đ°¸