��Ŀ����
����Ŀ��̽����֪��
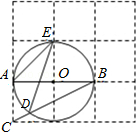
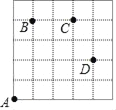
��ͼ1������OC��![]() ���ڲ���ͼ�й���3���ǣ�
���ڲ���ͼ�й���3���ǣ�![]() ��
��![]() ��
��![]() ����������һ���ǵĶ�������һ���Ƕ������������������OC��
����������һ���ǵĶ�������һ���Ƕ������������������OC��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
��1��һ���ǵ�ƽ����______����ǵġ��ɷ��ߡ���![]() ��ǡ����ǡ�
��ǡ����ǡ�![]()
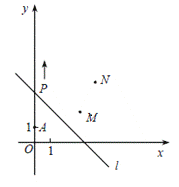
��2����ͼ2����![]() ��������PQ��
��������PQ��![]() �ġ��ɷ��ߡ�����
�ġ��ɷ��ߡ�����![]() ______��
______��![]() �ú�
�ú�![]() �Ĵ���ʽ��ʾ�����п��ܵĽ��
�Ĵ���ʽ��ʾ�����п��ܵĽ��![]()
�������
��ͼ2����![]() ��������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��
��������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��![]() ���ٶ���ʱ����ת����PQ��PN��
���ٶ���ʱ����ת����PQ��PN��![]() ʱֹͣ��ת����ת��ʱ��Ϊt�룮
ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��3����tΪ��ֵʱ������PM��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
��4��������PMͬʱ�Ƶ�P��ÿ��![]() ���ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ��
���ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ��![]() �ġ��ɷ��ߡ�ʱt��ֵ��
�ġ��ɷ��ߡ�ʱt��ֵ��



���𰸡��� ![]() ��
��![]() ��
��![]()
��������
![]() �����ɷ��߶��弴����⣻
�����ɷ��߶��弴����⣻
![]() ��3������������ɷ��߶��弴����⣻
��3������������ɷ��߶��弴����⣻
![]() ��3������������ɷ��߶���õ�������⼴�ɣ�
��3������������ɷ��߶���õ�������⼴�ɣ�
![]() ��3������������ɷ��߶���õ�������⼴�ɣ�
��3������������ɷ��߶���õ�������⼴�ɣ�
![]() һ���ǵ�ƽ����������ǵġ��ɷ��ߡ���
һ���ǵ�ƽ����������ǵġ��ɷ��ߡ���![]() ��ǡ����ǡ�
��ǡ����ǡ�![]()
�ʴ�Ϊ����
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��![]() ��
��
�������
![]() ��������
��������
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
�ʵ�tΪ9��12��18ʱ������PM��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
![]() ��������
��������
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
�ʵ�tΪ![]() ��4��6ʱ������PQ��
��4��6ʱ������PQ��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���