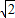Question

两圆半径分别是4cm和2cm，一条外公切线长为4cm，则两圆位置关系为（　　）

• A、外切
• B、内切
• C、外离
• D、相交

Answer 1

分析：求出两圆心之间的距离，再根据这个距离与两圆半径之和大小确定两圆位置关系．

解答：解：如图：
设两圆圆心分别为O和P，外公切线为AB，过P点作AB平行线交OA于C．
∵AB=4
∴PC=4
∵AO=4，PB=2
∴AC=2，OC=4-2=2．
在RT△CPO中
OP=

PC2+CO2

=

42+22

=

20

=2

5

＜4+2=6．
∴两圆位置关系为相交．
故选D．

点评：本题考查圆与圆的位置关系，同时考查了学生的综合应用能力及推理能力．