题目内容
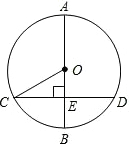
如图,矩形ABCD的两条边与圆相交于M、N、E、F四点,若AM=4,MN=5,DE=3,则EF的长是( )

| A.3.5 | B.5 | C.7 | D.8 |

过O作OH⊥AB于H,交CD与点G,
则EG=
EF,MH=
MN=
,
∵四边形ABCD是矩形,
∴DG=AH=AM+MH=4+
=
,
∵DE=3,
∴EG=
-3=
,
∴EF=2EG=2×
=7.
故选C.

则EG=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵四边形ABCD是矩形,
∴DG=AH=AM+MH=4+
| 5 |
| 2 |
| 13 |
| 2 |
∵DE=3,
∴EG=
| 13 |
| 2 |
| 7 |
| 2 |
∴EF=2EG=2×
| 7 |
| 2 |
故选C.


练习册系列答案
相关题目