题目内容
(2003•成都)已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.(1)求证:AC•BC=BE•CD;
(2)已知CD=6,AD=3,BD=8,求⊙O的直径BE的长.
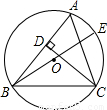
【答案】分析:(1)欲证AC•BC=BE•CD,可以证明△ADC∽△ECB得出;
(2)求⊙O的直径BE的长,由AC•BC=BE•CD知,可在Rt△ACD和Rt△BCD中,根据已知条件求出BC,AC的长即可.
解答: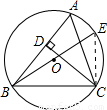 (1)证明:连接CE(1分)
(1)证明:连接CE(1分)
∵BE是⊙O的直径
∴∠ECB=90°
∵CD⊥AB
∴∠ADC=90°
∴∠ECB=∠ADC
又∵∠A=∠E(同弧所对的圆周角相等),
∴△ADC∽△ECB(2分)
∴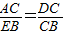
∴AC•BC=BE•CD;(1分)
(2)解:∵CD=6,AD=3,BD=8
∴BC=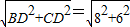 =10(1分)
=10(1分)
∴AC=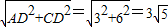 (1分)
(1分)
∵AC•BC=BE•CD
∴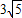 ×10=BE•6
×10=BE•6
∴BE=5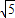
∴⊙O的直径BE的长是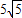 .(2分)
.(2分)
点评:本题考查了同弧所对的圆周角相等、直径所对的圆周角为直角及解直角三角形的知识,同时考查了相似三角形的判定和性质,综合性较强.
(2)求⊙O的直径BE的长,由AC•BC=BE•CD知,可在Rt△ACD和Rt△BCD中,根据已知条件求出BC,AC的长即可.
解答:
 (1)证明:连接CE(1分)
(1)证明:连接CE(1分)∵BE是⊙O的直径
∴∠ECB=90°
∵CD⊥AB
∴∠ADC=90°
∴∠ECB=∠ADC
又∵∠A=∠E(同弧所对的圆周角相等),
∴△ADC∽△ECB(2分)
∴
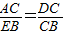
∴AC•BC=BE•CD;(1分)
(2)解:∵CD=6,AD=3,BD=8
∴BC=
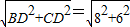 =10(1分)
=10(1分)∴AC=
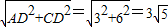 (1分)
(1分)∵AC•BC=BE•CD
∴
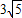 ×10=BE•6
×10=BE•6∴BE=5
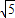
∴⊙O的直径BE的长是
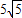 .(2分)
.(2分)点评:本题考查了同弧所对的圆周角相等、直径所对的圆周角为直角及解直角三角形的知识,同时考查了相似三角形的判定和性质,综合性较强.

练习册系列答案
相关题目
 (2003•成都)已知一次函数y1=kx+b的图象与反比例函数
(2003•成都)已知一次函数y1=kx+b的图象与反比例函数 (2003•成都)已知二次函数y=x2+bx+c的顶点M在直线y=-4x上,并且图象经过点A(-1,0).
(2003•成都)已知二次函数y=x2+bx+c的顶点M在直线y=-4x上,并且图象经过点A(-1,0). (2003•成都)已知:如图,在等腰梯形ABCD中,AD∥BC,PA=PD,求证:PB=PC.
(2003•成都)已知:如图,在等腰梯形ABCD中,AD∥BC,PA=PD,求证:PB=PC.