题目内容
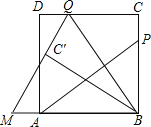
【题目】(10分)如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
【答案】(1)AP=BQ,理由参见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB即可;(2)过点Q作QH⊥AB于H,可得QH=BC=AB=3,∵BP=2PC,∴BP=2,PC=1,运用勾股定理可求得AP(即BQ)=![]() ,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
试题解析:(1)证明线段相等,通常证明所在的三角形全等,此题利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB,证明:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°,∴∠ABQ+∠CBQ=90°.∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ(同角的余角相等).∴△PBA≌△QCB(ASA),∴AP=BQ(全等三角形的对应边相等);(2)过点Q作QH⊥AB于H,如图:∵四边形ABCD是正方形,∴QH=BC=AB=3.∵BP=2PC,BP+PC=3,∴BP=2,PC=1,∵△PBA≌△QCB,∴CQ=BP=2,四边形QHCB是矩形,∴BH=CQ=2,∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,∴∠QBA=∠C′QB(等量代换),∴MQ=MB(等角对等边).设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中,根据勾股定理可得x2=(x﹣2)2+32,解得x=![]() .∴QM的长为
.∴QM的长为![]() ;
;
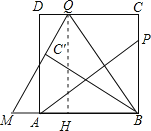
过点Q作QH⊥AB于H,如上题的思路可得:四边形ABCD是正方形,BP=m,PC=n,∴QH=BC=AB=m+n.∵△PBA≌△QCB,∴CQ=BP=m,四边形QHCB是矩形,∴BH=CQ=m.设QM=x,则有MB=QM=x,MH=x﹣m.在Rt△MHQ中,根据勾股定理可得x2=(x﹣m)2+(m+n)2,解得x=m+n+![]() ,∴AM=MB﹣AB=m+n+
,∴AM=MB﹣AB=m+n+![]() ﹣m﹣n=
﹣m﹣n=![]() .即AM的长为
.即AM的长为![]() .
.

【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.