Question

【题目】求解：如图，在△ABC中，∠A=42°，∠ABC和∠ACB的平分线相交于点D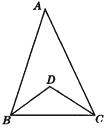

（1）求∠BDC的度数．
（2）在（1）中去掉∠A=42°这个条件，请探究∠BDC和∠A之间的数量关系．

Answer 1

【答案】
（1）

解答：∵∠ABC+∠ACB =180°-∠A=180°-42°=138°，

又∵BD，CD分别是∠ABC，∠ACB的平分线，

∴∠CBD=∠ABC，∠BCD=∠ACB，

∴∠CBD+∠BCD=（∠ABC+∠ACB）=69°，

∴∠BDC =180°-（∠CBD+∠BCD）=180°-69°=111°.

（2）

解答：90°+∠A.理由如下：

∵∠ABC+∠ACB =180°-∠A，

又∵BD，CD分别是∠ABC，∠ACB的平分线，

∴∠CBD=∠ABC，∠BCD=∠ACB，

∴∠CBD+∠BCD=（∠ABC+∠ACB）=（180°-∠A）=90°-∠A，

∴∠BDC =180°-（90°-∠A）=180°-90°+∠A=90°+∠A.

【解析】此题考查的是三角形的角平线的性质和三角形内角和定理．此题的关键是要求出∠A与（∠CBD+∠BCD）的数量关系.