题目内容
 如图,∠1=120°,∠BCD=60°,AD与BC为什么是平行的?(填空回答问题)
如图,∠1=120°,∠BCD=60°,AD与BC为什么是平行的?(填空回答问题)
将∠1的________角记为∠2
∵∠1+∠2=________,且∠1=120°( 已知)
∴∠2=________.
∵∠BCD=60°,(________)
∴∠BCD=∠________.
∴AD∥BC(________)
邻补角 180° 60° 已知 2 同位角相等,两直线平行
分析:首先记∠1的邻补角为∠2,得出∠2=60°,再由∠BCD=60°,得出∠BCD=∠2,从而得出AD∥BC.
解答:证明:将∠1的邻补角记为∠2.
∵∠1+∠2=180°,且∠1=120°( 已知),
∴∠2=60°,
∵∠BCD=60°( 已知),
∴∠BCD=∠2,
∴AD∥BC(同位角相等,两直线平行).
故答案分别为:邻补角,180°,60°,已知,2,同位角相等,两直线平行.
点评:此题考查的知识点是平行线的判定,关键是先由邻补角得出∠2=60°,再由已知得出∠BCD=∠2,从而得出AD∥BC.
分析:首先记∠1的邻补角为∠2,得出∠2=60°,再由∠BCD=60°,得出∠BCD=∠2,从而得出AD∥BC.
解答:证明:将∠1的邻补角记为∠2.
∵∠1+∠2=180°,且∠1=120°( 已知),
∴∠2=60°,
∵∠BCD=60°( 已知),
∴∠BCD=∠2,
∴AD∥BC(同位角相等,两直线平行).
故答案分别为:邻补角,180°,60°,已知,2,同位角相等,两直线平行.
点评:此题考查的知识点是平行线的判定,关键是先由邻补角得出∠2=60°,再由已知得出∠BCD=∠2,从而得出AD∥BC.

练习册系列答案
相关题目

 菱形ABCD中,如图,∠BAD=120°,AB=10cm,则AC=
菱形ABCD中,如图,∠BAD=120°,AB=10cm,则AC= 5、如图,∠1=120°,∠E=70°,∠A的大小是( )
5、如图,∠1=120°,∠E=70°,∠A的大小是( )
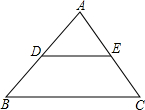 如图,∠DEC=120°,∠ACB=60°,∠B=50°,则∠ADE=
如图,∠DEC=120°,∠ACB=60°,∠B=50°,则∠ADE=