Question

【题目】如图，已知是的直径，弦于点，点在上，.

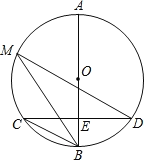
（1）判断、的位置关系，并说明理由；

（2）若，，求线段的长；

（3）若恰好经过圆心，求的度数.

Answer 1

【答案】（1）；（2）16；（3）30°

【解析】

（1）根据圆周角定理可得出∠M=∠D=∠C，由此即可得出结论；

（2）先根据AE=16，BE=4得出OB的长，进而得出OE的长，连接OC，根据勾股定理得出CE的长，进而得出结论；

（3）根据题意画出图形，根据圆周角定理可知，∠M=∠BOD，由∠M=∠D可知∠D=∠BOD，故可得出∠D的度数．

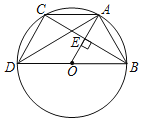
（1）BC∥MD．理由如下：

∵∠M=∠D，∠M=∠C，∴∠D=∠C，∴BC∥MD；

（2）连接OC．

∵AE=16，BE=4，∴OB==10，∴OE=10﹣4=6．

∵CD⊥AB，∴CE=CD．在Rt△OCE中，∵OE2+CE2=OC2，即62+CE2=102，解得：CE=8，∴CD=2CE=16；

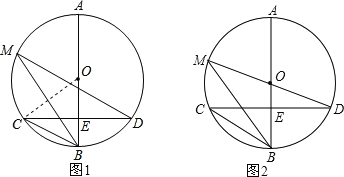
（3）如图2．

∵∠M=∠BOD，∠M=∠D，∴∠D=∠BOD，即∠BOD=2∠D．

∵AB⊥CD，∴∠BOD+∠D=90°，即3∠D=90°，解得：∠D=30°．