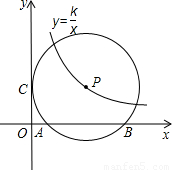
题目内容
已知圆P的圆心P在反比例函数 (k>0)第一象限图象上,并与x轴相交于A、B两点,且始终与y轴相切于定点C(0,1).
(k>0)第一象限图象上,并与x轴相交于A、B两点,且始终与y轴相切于定点C(0,1).(1)求实数k的取值范围;
(2)求经过A、B、C三点的二次函数图象的解析式;
(3)若二次函数图象的顶点为D,问是否存在实数k,使四边形ADBP为菱形?若存在,求出k的值;若不存在,说明理由;
(4)此抛物线的顶点D是否可能在圆P内?并证明你的结论.
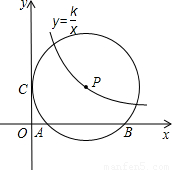
【答案】分析:(1)连接PC、PA、PB,过P点作PH⊥x轴,垂足为H,P的坐标是(k,1),得到PA=PC=k,由PA>PH即可得到答案;
(2)根据勾股定理得到AH= ,得到A(k-
,得到A(k- ,0),由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,得到B(k+
,0),由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,得到B(k+ ,0),可设该抛物线解析式为y=a(x-k)2+h,代入得到方程组
,0),可设该抛物线解析式为y=a(x-k)2+h,代入得到方程组 求出即可;
求出即可;
(3)抛物线顶点D坐标为(k,1-k2),根据四边形ADBP为菱形.则必有PH=DH,得到k2-1=1,求出即可;
(4)根据PD=1-(1-k2)=k2>k=PA,判断即可.
解答: 解:(1)连接PC、PA、PB,过P点作PH⊥x轴,垂足为H,
解:(1)连接PC、PA、PB,过P点作PH⊥x轴,垂足为H,
∵P点在反比例函数 的图象上,
的图象上,
∴P的坐标是(k,1),
∴PA=PC=k,在Rt△PAH中,由PA>PH,
解得:k>1,
答:实数k的取值范围是k>1.
(2)解:在Rt△APH中,AH= =
= ,
,
∴OA=OH-AH=k- ,
,
∴A(k- ,0),
,0),
∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,
∴OB=OA+2AH=k- +2
+2 =k+
=k+ ,
,
∴B(k+ ,0),
,0),
故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k,
可设该抛物线解析式为y=a(x-k)2+h,
又抛物线过C(0,1),B(k+ ,0),
,0),
得: ,
,
解得a=1,h=1-k2,
∴抛物线解析式为y=(x-k)2+1-k2,
答:经过A、B、C三点的二次函数图象的解析式是y=(x-k)2+1-k2.
(3)解:由(2)知抛物线顶点D坐标为(k,1-k2),
∴DH=k2-1,
若四边形ADBP为菱形.则必有PH=DH,
∵PH=1,
∴k2-1=1,
又∵k>1,
∴k=
∴当k取 时,PD与AB互相垂直平分,则四边形ADBP为菱形,
时,PD与AB互相垂直平分,则四边形ADBP为菱形,
答:存在实数k,使四边形ADBP为菱形,k的值是 .
.
(4)答:D点不可能在圆P内,
证明:∵PD=1-(1-k2)=k2>k=PA(圆P的半径),
所以D点不可能在圆P内.
点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的三种形式,二次函数图象上点的坐标特征,菱形的性质,勾股定理,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
(2)根据勾股定理得到AH=
 ,得到A(k-
,得到A(k- ,0),由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,得到B(k+
,0),由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,得到B(k+ ,0),可设该抛物线解析式为y=a(x-k)2+h,代入得到方程组
,0),可设该抛物线解析式为y=a(x-k)2+h,代入得到方程组 求出即可;
求出即可;(3)抛物线顶点D坐标为(k,1-k2),根据四边形ADBP为菱形.则必有PH=DH,得到k2-1=1,求出即可;
(4)根据PD=1-(1-k2)=k2>k=PA,判断即可.
解答:
 解:(1)连接PC、PA、PB,过P点作PH⊥x轴,垂足为H,
解:(1)连接PC、PA、PB,过P点作PH⊥x轴,垂足为H,∵P点在反比例函数
 的图象上,
的图象上,∴P的坐标是(k,1),
∴PA=PC=k,在Rt△PAH中,由PA>PH,
解得:k>1,
答:实数k的取值范围是k>1.
(2)解:在Rt△APH中,AH=
 =
= ,
,∴OA=OH-AH=k-
 ,
,∴A(k-
 ,0),
,0),∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB,
∴OB=OA+2AH=k-
 +2
+2 =k+
=k+ ,
,∴B(k+
 ,0),
,0),故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k,
可设该抛物线解析式为y=a(x-k)2+h,
又抛物线过C(0,1),B(k+
 ,0),
,0),得:
 ,
,解得a=1,h=1-k2,
∴抛物线解析式为y=(x-k)2+1-k2,
答:经过A、B、C三点的二次函数图象的解析式是y=(x-k)2+1-k2.

(3)解:由(2)知抛物线顶点D坐标为(k,1-k2),
∴DH=k2-1,
若四边形ADBP为菱形.则必有PH=DH,
∵PH=1,
∴k2-1=1,
又∵k>1,
∴k=

∴当k取
 时,PD与AB互相垂直平分,则四边形ADBP为菱形,
时,PD与AB互相垂直平分,则四边形ADBP为菱形,答:存在实数k,使四边形ADBP为菱形,k的值是
 .
.(4)答:D点不可能在圆P内,
证明:∵PD=1-(1-k2)=k2>k=PA(圆P的半径),
所以D点不可能在圆P内.
点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的三种形式,二次函数图象上点的坐标特征,菱形的性质,勾股定理,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

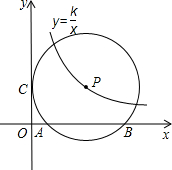 ,且始终与y轴相切于定点C(0,1).
,且始终与y轴相切于定点C(0,1). (k>1)图象上,并与x轴相交于A、B两点.且始终与y轴相切于定点C(0,1).
(k>1)图象上,并与x轴相交于A、B两点.且始终与y轴相切于定点C(0,1).
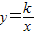 (k>0)第一象限图象上,并与x轴相交于A、B两点,且始终与y轴相切于定点C(0,1).
(k>0)第一象限图象上,并与x轴相交于A、B两点,且始终与y轴相切于定点C(0,1).