题目内容
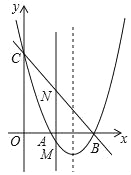
【题目】如图，已知
为
外心，
为
上一点，
与
的交点为
，且
．
①求证：
；
②若
，且的半径为
，
为
内心，求
的长．
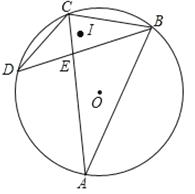
【答案】①证明见解析； ②
【解析】
①先求出
，然后求出△BCE和△ACB相似，根据相似三角形对应角相等可得∠A=∠CBE，再根据在同圆或等圆中，同弧所对的圆周角相等可得∠A=∠D，然后求出∠D=∠CBE，然后根据等角对等边即可得证；
②连接OB、OC，根据在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍求出∠BOC=60°，然后判定△OBC是等边三角形，再根据等腰三角形三线合一的性质以及三角形的内心的性质可得OC经过点I，设OC与BD相交于点F，然后求出CF，再根据I是三角形的内心，利用三角形的面积求出IF，然后求出CI，最后根据OI=OC﹣CI计算即可得解．
①∵BC2=ACCE，∴．
∵∠BCE=∠ECB，∴△BCE∽△ACB，∴∠CBE=∠A．
∵∠A=∠D，∴∠D=∠CBE，∴CD=CB；
②连接OB、OC．
∵∠A=30°，∴∠BOC=2∠A=2×30°=60°．
∵OB=OC，∴△OBC是等边三角形．
∵CD=CB，I是△BCD的内心，∴OC经过点I，设OC与BD相交于点F，则CF=BC×sin30°
BC，BF=BCcos30°
BC，所以，BD=2BF=2
BC
BC，设△BCD内切圆的半径为r，则S△BCDBDCF（BD+CD+BC）r，即
BCBC（BC+BC+BC）r，解得：r
BC
BC，即IFBC，所以，CI=CF﹣IFBC
BC=（2
）BC，OI=OC﹣CI=BC﹣（2）BC=（
1）BC．
∵⊙O的半径为3
，∴BC=3，∴OI=（1）（3）=3
3﹣3
．
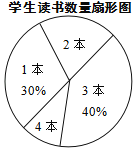
一线名师提优试卷系列答案【题目】某校七年级共有500名学生，在“世界读书日”前夕，开展了“阅读助我成长”的读书活动．为了解该年级学生在此次活动中课外阅读情况，童威随机抽取m名学生，调查他们课外阅读书籍的数量，将收集的数据整理成如下统计表和扇形图．
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
（1）直接写出m、a、b的值；
（2）估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本？
