题目内容
已知:二次函数y=(2m-1)x2-(5m+3)x+3m+5
(1)m为何值时,此抛物线必与x轴相交于两个不同的点;
(2)m为何值时,这两个交点在原点的左右两边;
(3)m为何值时,此抛物线的对称轴是y轴;
(4)m为何值时,这个二次函数有最大值 .
.
解:(1)∵△=(5m+3)2-4(2m-1)(3m+5)=m2+2m+29>0,
∴当 时,此抛物线必与x轴相交于两个不同的点;
时,此抛物线必与x轴相交于两个不同的点;
(2)根据题意,得
 <0,
<0,
则 ;
;
(3)根据题意,得
3m+5=0,
则m=- ;
;
(4)根据题意,得
 =-
=- ,
,
化简,得m2-8m+34=0,
此方程无实数根,
则不存在.
分析:(1)若抛物线必与x轴相交于两个不同的点,则△>0,且2m-1≠0;
(2)若抛物线与x轴的两个交点在原点的左右两边,则需 <0即可;
<0即可;
(3)若抛物线的对称轴是y轴,则b=0;
(4)根据a<0时,二次函数的最大值是 进行求解.
进行求解.
点评:此题考查了二次函数的图象与一元二次方程之间的联系,同时要熟悉抛物线的顶点坐标公式.
∴当
 时,此抛物线必与x轴相交于两个不同的点;
时,此抛物线必与x轴相交于两个不同的点;(2)根据题意,得
 <0,
<0,则
 ;
;(3)根据题意,得
3m+5=0,
则m=-
 ;
;(4)根据题意,得
 =-
=- ,
,化简,得m2-8m+34=0,
此方程无实数根,
则不存在.
分析:(1)若抛物线必与x轴相交于两个不同的点,则△>0,且2m-1≠0;
(2)若抛物线与x轴的两个交点在原点的左右两边,则需
 <0即可;
<0即可;(3)若抛物线的对称轴是y轴,则b=0;
(4)根据a<0时,二次函数的最大值是
 进行求解.
进行求解.点评:此题考查了二次函数的图象与一元二次方程之间的联系,同时要熟悉抛物线的顶点坐标公式.

练习册系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.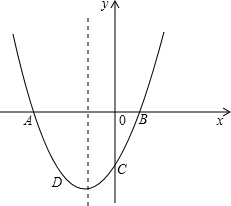 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.