题目内容
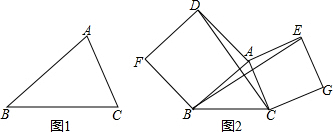
18.(1)如图1:已知△ABC中,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法.但要保留作图痕迹).(2)如图2,已知△ABC中,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,判断BE与CD有什么数量关系,并加以证明.
分析 (1)分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE即可;
(2)BE与CD数量关系是相等,由正方形的性质就可以得出△ADC≌△ABE,根据全等三角形的性质即可得到CD=BE.
解答 解:(1)如图所示: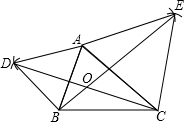
(2)解:CD=BE.
理由如下:
∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE(SAS),
∴CD=BE.
点评 此题考查了全等三角形的判定与性质,等边三角形的性质以及基本作图,正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
9.若点(-1,y1),(-2,y2),(2,y3)在反比例函数$y=-\frac{{{k^2}+1}}{x}$图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
6.下列每组数分别是三根小木棒的长度(cm),用它们能摆成三角形的是( )
| A. | 3 4 9 | B. | 2 3 5 | C. | 5 12 13 | D. | 5 5 11 |
3.点A(-1,y1),B(2,y2)在双曲线$y=\frac{1}{x}$上,则y1,y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
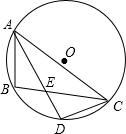 如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.
如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.