题目内容
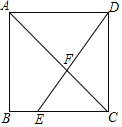
【题目】如图，在正方形ABCD中，E是边BC上一点，且BE：CE＝1：3，DE交AC于点F，若DE＝10，则CF等于( )
A. 
B. 
C. 
D. 
【答案】A
【解析】
由BE：CE＝1：3，即可找到EC：BC＝3：4，从而可求得EC、DC的长，则可以求得AC，易证得△FEC∽△FDA，则可求AF与CF的比例关系，最后求得FC．
解：∵四边形ABCD为正方形，
∴BC＝DC
∵BE：CE＝1：3，
∴EC：BC＝3：4
∵DE＝10
∴设EC＝3x，则BC＝4x
在Rt△DCE中，有100＝(3x)2+(4x)2，解得x＝2
则EC＝6，DC＝8
同理得，AC＝8
∵易证△FEC∽△FDA
∴
,
∴FA＝
FC
∵AC＝AF+FC
∴8＝FC+FC，
得FC＝
故选：A．
练习册系列答案
相关题目
