题目内容
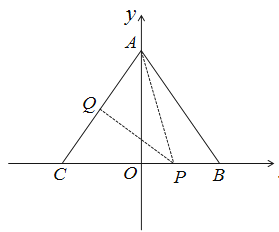
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标为
的三个顶点坐标为![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是二元一次方程组
是二元一次方程组![]() 的解,且
的解,且![]() .
.
(1)求![]() 的面积;
的面积;
(2)动点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 向终点
向终点![]() 运动,连接
运动,连接![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() (
(![]() ),求
),求![]() 与
与![]() 之间的关系式,并直接写出
之间的关系式,并直接写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当![]() 时,求点
时,求点![]() 的坐标;此时若在边
的坐标;此时若在边![]() 上存在一点
上存在一点![]() ,连接
,连接![]() ,使
,使![]() ,试判断
,试判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
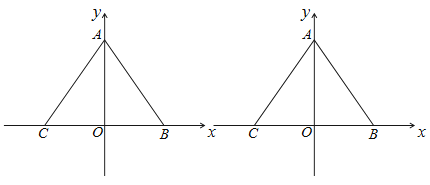
【答案】(1)12 (2)![]() (3)
(3)![]() ,
,![]() ,证明见解析
,证明见解析
【解析】
(1)解二元一次方程组解出m,n的值,即可得出A、B、C的坐标,即可得出![]() 的面积;
的面积;
(2)根据各点的坐标得![]() ,即可确定
,即可确定![]() 的取值范围,再根据三角形的面积公式列出关系式即可;
的取值范围,再根据三角形的面积公式列出关系式即可;
(3)用t表示△APC的面积,根据![]() 联立方程解得
联立方程解得![]() ,即可得到点P的坐标,根据三角形外角的性质即可求出
,即可得到点P的坐标,根据三角形外角的性质即可求出![]() 与
与![]() 的数量关系.
的数量关系.
(1)![]()
解得![]()
∴![]() ,
,![]() ,
,![]()
![]() .
.
(2)∵![]() ,
,![]() ,
,![]()
∴![]()
∵动点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 向终点
向终点![]() 运动
运动
∴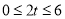
解得![]()
当![]() 时,
时,![]()
故![]() .
.
(3)∵![]() ,
,![]()
∴当![]() 时,
时,![]()
解得![]() 成立
成立
∴![]()
∴![]()
如图,作![]() ,连接PQ、AP
,连接PQ、AP
∵![]() ,
,![]() ,
,
![]()
∴![]()
∵![]()
∴![]()
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目