Question

如图，直角三形纸片ABC中，∠ACB=90°，AC=6，BC=8．折叠该纸片使点B与点C重合，折痕与AB、BC的交点分别为D、E．则sin∠DAE=________．

Answer 1

分析：作EF⊥AB于点F，首先求得AB的长，△ABE的面积．以及三角形的面积公式即可求得EF的长，在直角△ACE中，利用勾股定理即可求得AE的长，然后在直角△AEF中，利用三角函数的定义即可求得．
解答：解：作EF⊥AB于点F．
∵点B与点C重合，
∴DE是BC的中垂线，
∴CE=BC=×8=4，
在直角△ACE中，AE===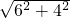2，
在直角△ABC中，AB==10，
∵S_△ABC=AC•BC=×6×8=24，AE=BE，
∴S_△ABE=S_△ABC=AB•EF=12，
∴EF=，
∴sin∠DAE===．
故答案是：．
点评：本题是三角形的折叠、勾股定理以及三角函数的综合题，正确理解三角函数的定义作出辅助线，求得EF的长是关键．