题目内容
若三角形的三边长分别是3，1-2a，8，求a的取值范围并在数轴上表示出来．
解：由三角形三边关系定理得8-3＜1-2a＜8+3，即-5＜a＜-2．
即a的取值范围是-5＜a＜-2．
在数轴上表示为：
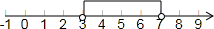
分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边；即可求a的取值范围，再将a的取值范围在数轴上表示出来即可．
点评：考查了求范围的问题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
即a的取值范围是-5＜a＜-2．
在数轴上表示为：
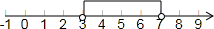
分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边；即可求a的取值范围，再将a的取值范围在数轴上表示出来即可．
点评：考查了求范围的问题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
练习册系列答案
相关题目
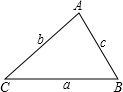在一块锐角三角形的余料上，加工成正方形零件，使正方形的4个顶点都在三角形边上，若三角形的三边长分别为a、b、c，且a＞b＞c，问正方形的2个顶点放在哪条边上可使加工出来的正方形零件面积最大？