题目内容
 如图,将三个全等的正方形拼成一个矩形ADHE,则:∠ABE+∠ACE+∠ADE等于________度.
如图,将三个全等的正方形拼成一个矩形ADHE,则:∠ABE+∠ACE+∠ADE等于________度.
90
分析:设正方形的边长为1,根据正方形的性质得到∠ABE=45°,BE= ,再利用勾股定理计算出CE=
,再利用勾股定理计算出CE= ,DE=
,DE= ,则BE:BD=BC:BE=
,则BE:BD=BC:BE= :2,加上公共角,于是可判断△CBE∽△EBD,则∠BDE=∠BEC,再利用三角形外角性质得∠ABE=∠BEC+∠BCE=45°,然后计算∠ABE+∠ACE+∠ADE.
:2,加上公共角,于是可判断△CBE∽△EBD,则∠BDE=∠BEC,再利用三角形外角性质得∠ABE=∠BEC+∠BCE=45°,然后计算∠ABE+∠ACE+∠ADE.
解答:设正方形的边长为1,
∵四边形AEFB为正方形,
∴∠ABE=45°,BE= ,
,
在Rt△AEC中,AC=2
∴CE= =
= ,
,
在Rt△AED中,AD=3,
∴DE= =
= ,
,
∴BE:BD= :2,BC:BE=1:
:2,BC:BE=1: =
= :2,
:2,
∴BE:BD=BC:BE,
而∠CBE=∠EBD,
∴△CBE∽△EBD,
∴∠BDE=∠BEC,
∵∠ABE=∠BEC+∠BCE=45°,
∴∠ABE+∠ACE+∠ADE=45°+45°=90°.
故答案为90.
点评:本题考查了相似三角形得判定与性质:如果两个三角形的两条对应边的比相等,且它们所夹的角也相等,那么这两个三角形相似;相似三角形对应角相等,对应边的比相等.也考查了勾股定理以及正方形的性质.
分析:设正方形的边长为1,根据正方形的性质得到∠ABE=45°,BE=
 ,再利用勾股定理计算出CE=
,再利用勾股定理计算出CE= ,DE=
,DE= ,则BE:BD=BC:BE=
,则BE:BD=BC:BE= :2,加上公共角,于是可判断△CBE∽△EBD,则∠BDE=∠BEC,再利用三角形外角性质得∠ABE=∠BEC+∠BCE=45°,然后计算∠ABE+∠ACE+∠ADE.
:2,加上公共角,于是可判断△CBE∽△EBD,则∠BDE=∠BEC,再利用三角形外角性质得∠ABE=∠BEC+∠BCE=45°,然后计算∠ABE+∠ACE+∠ADE.解答:设正方形的边长为1,
∵四边形AEFB为正方形,
∴∠ABE=45°,BE=
 ,
,在Rt△AEC中,AC=2
∴CE=
 =
= ,
,在Rt△AED中,AD=3,
∴DE=
 =
= ,
,∴BE:BD=
 :2,BC:BE=1:
:2,BC:BE=1: =
= :2,
:2,∴BE:BD=BC:BE,
而∠CBE=∠EBD,
∴△CBE∽△EBD,
∴∠BDE=∠BEC,
∵∠ABE=∠BEC+∠BCE=45°,
∴∠ABE+∠ACE+∠ADE=45°+45°=90°.
故答案为90.
点评:本题考查了相似三角形得判定与性质:如果两个三角形的两条对应边的比相等,且它们所夹的角也相等,那么这两个三角形相似;相似三角形对应角相等,对应边的比相等.也考查了勾股定理以及正方形的性质.

练习册系列答案
相关题目

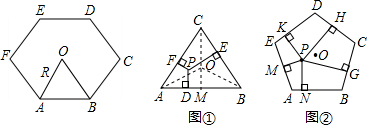 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?

 a(h1+h2+h3)
a(h1+h2+h3) ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°, ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60° AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60° a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60° ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°