Question

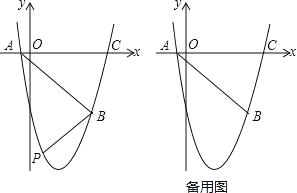
【题目】如图，已知直线 与x轴、y轴相交于P、Q两点，与y=的图像相交于A（－2，m）、B（1，n）两点，连接OA、OB. 给出下列结论： ①k1k2<0；②m+n=0； ③S△AOP= S△BOQ；④不等式k1x+b＞的解集是x<－2或0<x<1，其中正确的结论的序号是 .

Answer 1

【答案】②③④.

【解析】

试题分析：①由直线 的图像在二、四象限，知k1<0；y=的图像在二、四象限，知k2<0；因此k1k2＞0，所以①错误；②A，B两点在y=的图像上，故将A（－2，m）、B（1，n）代入，得m=，n= k2；从而得出m+n=0，故②正确；③令x=0，则y=b，所以Q（0，b），则S△BOQ=×1×｜b｜= -b；将A（－2，m）、B（1，n）分别代入，解得k1=，所以y=x+b；令y=0，则x=-b，所以P（-b，0），则S△AOP=×|-2|×｜-b｜= -b；所以S△AOP= S△BOQ，故③正确；④由图像知，在A点左边，不等式k1x+b的图像在的图像的上边，故满足k1x+b＞；在Q点与A点之间，不等式k1x+b的图像在的图像的上边，故满足k1x+b＞；因此不等式k1x+b＞的解集是x<－2或0<x<1. 故④正确.