题目内容
当三个非负实数x、y、z满足关系式x+3y+2z=3与3x+3y+z=4时,M=3x-2y+4z的最小值和最大值分别是( )
分析:根据关系式x+3y+2z=3与3x+3y+z=4求出y和z与x的关系式,又因x、y、z均为非负实数,求出x的取值范围,于是可以求出M的最大值和最小值.
解答:解:由
得:
,
代入M的表达式中得,
M=3x-2y+4z=3x-
(1-x)+4(2x-1)=
x-
,
又因x、y、z均为非负实数,
所以
≥0,
即
≤x≤1,
当x=
时,M有最小值为-
,
当x=1时,M有最大值为7.
故选B.
|
|
代入M的表达式中得,
M=3x-2y+4z=3x-
| 10 |
| 3 |
| 43 |
| 3 |
| 22 |
| 3 |
又因x、y、z均为非负实数,
所以
|
即
| 1 |
| 2 |
当x=
| 1 |
| 2 |
| 1 |
| 6 |
当x=1时,M有最大值为7.
故选B.
点评:本题主要考查函数最值问题的知识点,解答本题的关键是把y和z用x表示出来,此题难度不大.

练习册系列答案
相关题目
 +
+ -1,例如:把(1,2)放入其中,就会得到
-1,例如:把(1,2)放入其中,就会得到 +
+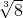 -1=2,现将实数对(m,16)放入其中,得到实数5,那么m的值是________.
-1=2,现将实数对(m,16)放入其中,得到实数5,那么m的值是________. ; ②
; ② ______
______ ③8+8______
③8+8______
 ;
; ,∴
,∴ ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. ,并指出等号成立时的条件.
,并指出等号成立时的条件.