题目内容
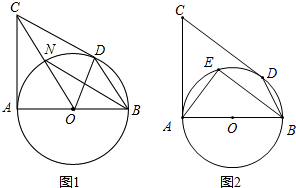 如图,已知CA、CD是⊙O的两条切线,A、D为切点,AB是⊙O的直径.
如图,已知CA、CD是⊙O的两条切线,A、D为切点,AB是⊙O的直径.(1)如图1,OC交⊙O于N,若BN∥CD,求证:BN=CD;
(2)如图2,BE∥CD交⊙O于E,若AB=AC=8,求BE的长.
考点:切线的性质
专题:
分析:(1)如图1,连接AD,利用切线的性质及四点共圆的知识问题即可解决;
(2)如图2,作辅助线,证明△CAG≌△ABE,得AE=CG;运用切线的性质及勾股定理即可解决问题.
(2)如图2,作辅助线,证明△CAG≌△ABE,得AE=CG;运用切线的性质及勾股定理即可解决问题.
解答: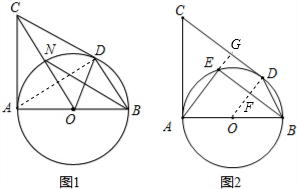 解:(1)如图1,连接AD;
解:(1)如图1,连接AD;
CA、CD是⊙O的两条切线,
∴∠CAO+∠CDO=90°+90°=180°,
∴C、A、O、D四点共圆,
∴∠CAO=∠CDA;
又∵CD为⊙O的切线,
∴∠ABD=∠CDA,
∴∠COA=∠ABD,
∴CO∥BD;
又∵BN∥CD,
∴四边形DCNB为平行四边形,
∴BN=CD.
(2)如图2,延长AE交CD于点G,连接OD,交BE于点F;
∵AB⊙O的直径,CD为⊙O的切线,
∴AE⊥BE,CD⊥OD;
又∵CD∥BE,
∴CD⊥AG,OD⊥BE;
∴四边形EFDG为矩形,EF=DG;
∴OF∥AE,而OA=OB,
∴BF=EF;
∵∠C+∠CAG=∠CAG+∠EAB=90°,
∴∠C=∠EAB;
在△CAG与△ABE中,
,
∴△CAG≌△ABE(AAS),
∴CG=AE(设为x),AG=BE;
∵CA、CD分别为⊙O的切线,
∴CA=CD=8,DG=8-x,
∴EF=DG=8-x;
∴BE=2EF=16-2x;
由勾股定理得:
82=x2+(16-2x)2,
整理得:5x2-64x+192=0,
解得:x=
或8(舍去),
∴BE=16-2x=
,
即BE的长为
.
 解:(1)如图1,连接AD;
解:(1)如图1,连接AD;CA、CD是⊙O的两条切线,
∴∠CAO+∠CDO=90°+90°=180°,
∴C、A、O、D四点共圆,
∴∠CAO=∠CDA;
又∵CD为⊙O的切线,
∴∠ABD=∠CDA,
∴∠COA=∠ABD,
∴CO∥BD;
又∵BN∥CD,
∴四边形DCNB为平行四边形,
∴BN=CD.
(2)如图2,延长AE交CD于点G,连接OD,交BE于点F;
∵AB⊙O的直径,CD为⊙O的切线,
∴AE⊥BE,CD⊥OD;
又∵CD∥BE,
∴CD⊥AG,OD⊥BE;
∴四边形EFDG为矩形,EF=DG;
∴OF∥AE,而OA=OB,
∴BF=EF;
∵∠C+∠CAG=∠CAG+∠EAB=90°,
∴∠C=∠EAB;
在△CAG与△ABE中,
|
∴△CAG≌△ABE(AAS),
∴CG=AE(设为x),AG=BE;
∵CA、CD分别为⊙O的切线,
∴CA=CD=8,DG=8-x,
∴EF=DG=8-x;
∴BE=2EF=16-2x;
由勾股定理得:
82=x2+(16-2x)2,
整理得:5x2-64x+192=0,
解得:x=
| 24 |
| 5 |
∴BE=16-2x=
| 32 |
| 5 |
即BE的长为
| 32 |
| 5 |
点评:本题在考查切线的性质及其应用的同时,还渗透了对四点共圆、平行线的判定、勾股定理的应用等知识点的考查;灵活运用有关定理来解题是关键.

练习册系列答案
相关题目
关于有理数的分类正确的是( )
| A、正数和负数统称有理数 |
| B、正整数、负整数统称整数 |
| C、正整数和负整数还有负分数和正分数统称有理数 |
| D、整数和分数统称有理数 |
若m、n、p是正整数,则(am•an)p等于( )
| A、am•anp |
| B、amp+np |
| C、amnp |
| D、amp•an |
下列方程是一元二次方程的是( )
A、x2+3x-
| ||
| B、x2+x-4=x2 | ||
C、x2=
| ||
| D、y2-x+=0 |
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.
如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长. 如图,已知点A、B为数轴上分别表示互为相反数的两个点,且A、B两点之间的距离为5,则A、B表示的数分别为
如图,已知点A、B为数轴上分别表示互为相反数的两个点,且A、B两点之间的距离为5,则A、B表示的数分别为