题目内容
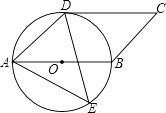
【题目】![]() 中,三个内角的平分线交于点
中,三个内角的平分线交于点![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .
.
(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想![]() 与
与![]() 的关系,并说明你的理由;
的关系,并说明你的理由;

【答案】(1) 110°, 110°(2)相等,证明见解析
【解析】
(1)根据内角和的性质得出∠BAC+∠BCA=180°-∠ABC=140°,
再利用角平分线的性质得到∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,再根据三角形的内角和即可求出∠AOC;根据∠ADO是△BDO的一个外角即可求出其度数;
(∠BAC+∠BCA)=70°,再根据三角形的内角和即可求出∠AOC;根据∠ADO是△BDO的一个外角即可求出其度数;
(2)设∠ABC=a,根据①的方法求出∠AOC与∠ADO即可判断
(1)∵∠ABC=40°,∴∠BAC+∠BCA=180°-∠ABC=140°,
∵三个内角的平分线交于点![]() ,∴∠OAC+∠OCA=
,∴∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,
(∠BAC+∠BCA)=70°,
∠AOC=180°-(∠OAC+∠OCA)=110°,
∵∠ADO是△BDO的一个外角,![]()
∴∠ADO=∠ABO+90°=![]() ∠ABC+90°=110°.
∠ABC+90°=110°.
(2)相等,证明如下:
设∠ABC=a,
根据①的方法求出∠AOC=180°-(∠OAC+∠OCA)
=180°-![]() (∠BAC+∠BCA)
(∠BAC+∠BCA)
= 180°-![]() (180°-a)
(180°-a)
=90°+![]() a
a
∠ADO =∠ABO+90°
=![]() ∠ABC+90°
∠ABC+90°
=![]() a+90°
a+90°
故![]() =
=![]()

练习册系列答案
相关题目