题目内容
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=
m，斜面坡角为30°，求木箱端点E距地面AC的高度EF．
| 3 |
连接AE，
在Rt△ABE中，AB=3m，BE=
m，
则AE=
=2
m，
又∵tan∠EAB=
=
，
∴∠EAB=30°，
在Rt△AEF中，∠EAF=∠EAB+∠BAC=60°，
∴EF=AE×sin∠EAF=2
×
=3m．
答：木箱端点E距地面AC的高度为3m．
在Rt△ABE中，AB=3m，BE=
| 3 |
则AE=
| AB2+BE2 |
| 3 |
又∵tan∠EAB=
| BE |
| AB |
| ||
| 3 |
∴∠EAB=30°，
在Rt△AEF中，∠EAF=∠EAB+∠BAC=60°，
∴EF=AE×sin∠EAF=2
| 3 |
| ||
| 2 |
答：木箱端点E距地面AC的高度为3m．
练习册系列答案
相关题目
（2013•丽水）一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=
m，已知木箱高BE=
m，斜坡角为30°，则木箱端点E距地面AC的高度EF为 m．
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=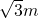
，斜面坡角为30°，求木箱端点E距地面AC的高度EF．
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=
，斜面坡角为30°，求木箱端点E距地面AC的高度EF．