题目内容
甲、乙两个盒子中装有质地、大小相同的小球.甲盒中有2个白球、1个黄球和1个蓝球;乙盒中有1个白球、2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
(1)求乙盒中蓝球的个数;
(2)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
解:(1)设乙盒中有x个蓝球,则从乙盒中任意摸取一球,摸得蓝球的概率为:P1=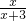 ,
,
从甲盒中任意摸取一球,摸得蓝球的概率P2= ;
;
∵从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
依题意得: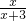 =
= ,
,
解得:x=3,
经检验:x=3是原方程的根,
∴乙盒中蓝球的个数是3个;
(2)列表得:
∴可能的结果有24,其中均为蓝球的有3种,
∴从甲、乙两盒中分别任意摸取一球,这两球均为蓝球的概率为 =
= .
.
分析:(1)由甲盒中有2个白球、1个黄球和1个蓝球,即可求得从甲盒中任意摸取一球,摸得篮球的概率,又由乙盒中有1个白球、2个黄球和若干个蓝球,可设乙盒中有x个篮球,则可求得从乙盒中任意摸取一球,摸得篮球的概率,根据从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍,列方程即可求得答案;
(2)采用列表法或树状图法,求得所有可能的结果与符合条件的情况数目;二者的比值就是其发生的概率.
点评:本题考查的是用列表法或画树状图法求概率与古典概率的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
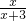 ,
,从甲盒中任意摸取一球,摸得蓝球的概率P2=
 ;
;∵从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
依题意得:
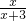 =
= ,
,解得:x=3,
经检验:x=3是原方程的根,
∴乙盒中蓝球的个数是3个;
(2)列表得:
| 乙 甲 | 白 | 黄1 | 黄2 | 蓝1 | 蓝2 | 蓝3 |
| 白1 | 白1,白 | 白1,黄1 | 白1,黄2 | 白1,蓝1 | 白1,蓝2 | 白1,蓝3 |
| 白2 | 白2,白 | 白2,黄1 | 白2,黄2 | 白2,蓝1 | 白2,蓝2 | 白2,蓝3 |
| 黄 | 黄,白 | 黄,黄1 | 黄,黄2 | 黄,蓝1 | 黄,蓝2 | 黄,蓝3 |
| 蓝 | 蓝,白 | 蓝,黄1 | 蓝,黄2 | 蓝,蓝1 | 蓝,蓝2 | 蓝,蓝3 |
∴从甲、乙两盒中分别任意摸取一球,这两球均为蓝球的概率为
 =
= .
.分析:(1)由甲盒中有2个白球、1个黄球和1个蓝球,即可求得从甲盒中任意摸取一球,摸得篮球的概率,又由乙盒中有1个白球、2个黄球和若干个蓝球,可设乙盒中有x个篮球,则可求得从乙盒中任意摸取一球,摸得篮球的概率,根据从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍,列方程即可求得答案;
(2)采用列表法或树状图法,求得所有可能的结果与符合条件的情况数目;二者的比值就是其发生的概率.
点评:本题考查的是用列表法或画树状图法求概率与古典概率的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目