题目内容
两圆外切,它们的外公切线互相垂直,如果大圆的半径为R,小圆的半径为r,那么 = .
= .
【答案】分析:首先根据题意作出图形,然后连接O1A,O2D,O1C,过点D作DF∥O1O2,易证得四边形O1O2DF是平行四边形,即可求得AF=R-r,DF=R+r,由切线的性质可得∠ACO1=45°,易得△ADF是等腰直角三角形,即可得DF=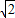 AF,继而求得
AF,继而求得 的值.
的值.
解答: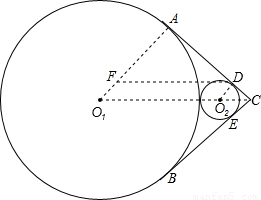 解:如图,⊙O1与⊙O2外切,AD,BE分别是外公切线,且AD⊥BE于点C,
解:如图,⊙O1与⊙O2外切,AD,BE分别是外公切线,且AD⊥BE于点C,
连接O1A,O2D,O1C,过点D作DF∥O1O2,
∴O1A⊥AD,O2D⊥AD,
∴O1A∥O2D,
∴四边形O1O2DF是平行四边形,
∴DF=012=R+r,O1F=O2D=r,
∴AF=O1A-O1F=R-r,
∵AC⊥BC,
∴∠ACO1=45°,
∴∠ADF=∠ACO1=45°,
∴∠AFD=∠ADF=45°,即△AFD为等腰直角三角形,
∴DF=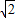 AF,
AF,
∴R+r=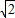 (R-r),
(R-r),
∴R=(3+2 )r,
)r,
∴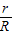 =
=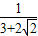 =3-2
=3-2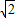 .
.
故答案为:3-2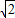 .
.
点评:此题考查了相切两圆的性质、平行四边形的判定与性质以及等腰直角三角形的性质.此题难度较大,解题的关键是根据题意作出图形,掌握数形结合思想的应用.
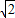 AF,继而求得
AF,继而求得 的值.
的值.解答:
 解:如图,⊙O1与⊙O2外切,AD,BE分别是外公切线,且AD⊥BE于点C,
解:如图,⊙O1与⊙O2外切,AD,BE分别是外公切线,且AD⊥BE于点C,连接O1A,O2D,O1C,过点D作DF∥O1O2,
∴O1A⊥AD,O2D⊥AD,
∴O1A∥O2D,
∴四边形O1O2DF是平行四边形,
∴DF=012=R+r,O1F=O2D=r,
∴AF=O1A-O1F=R-r,
∵AC⊥BC,
∴∠ACO1=45°,
∴∠ADF=∠ACO1=45°,
∴∠AFD=∠ADF=45°,即△AFD为等腰直角三角形,
∴DF=
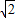 AF,
AF,∴R+r=
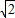 (R-r),
(R-r),∴R=(3+2
 )r,
)r,∴
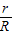 =
=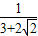 =3-2
=3-2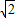 .
.故答案为:3-2
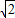 .
.点评:此题考查了相切两圆的性质、平行四边形的判定与性质以及等腰直角三角形的性质.此题难度较大,解题的关键是根据题意作出图形,掌握数形结合思想的应用.

练习册系列答案
相关题目